题目内容
请阅读材料:
①一般地,n个相同的因数a相乘:
记为an,如2•2•2=23=8,此时,3叫做以2为底8的对数,记为log28 (即log28=log223=3).
②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=logaan=n),如34=81,则4叫做以3为底81的对数,记为log381(即log381=log334=4).
(1)计算下列各对数的值:
log24=
(2)观察(1)题中的三数,4,16,64之间存在怎样的关系式
log24,log216,log264又存在怎样的关系式.
(3)由(2)题猜想 logaM+logaN=
①一般地,n个相同的因数a相乘:
| ||
| n个 |
②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=logaan=n),如34=81,则4叫做以3为底81的对数,记为log381(即log381=log334=4).
(1)计算下列各对数的值:
log24=
2
2
;log216=4
4
;log264=6
6
.(2)观察(1)题中的三数,4,16,64之间存在怎样的关系式
4×16=64
4×16=64
log24,log216,log264又存在怎样的关系式.
log24+log216=log264
log24+log216=log264
(3)由(2)题猜想 logaM+logaN=
logaMN
logaMN
(a>0且a≠1,M>0,N>0),并结合幂的运算法则:am•an=am+n加以证明.分析:(1)根据对数的定义,确定每个式子中对应的b是a的几次方,则式子的值就是几;
(2)根据4×16=64,即可写出关系式;
(3)根据(2)的结果即可直接写出结论,然后根据同底数的幂的乘法法则,证明logaam+logaan=logaam•an,即可证得.
(2)根据4×16=64,即可写出关系式;
(3)根据(2)的结果即可直接写出结论,然后根据同底数的幂的乘法法则,证明logaam+logaan=logaam•an,即可证得.
解答:(1)解:∵4=22,16=24,64=26,
∴log24=2;log216=4;log264=6;
(2)解:4,16,64之间存在怎样的关系式:4×16=64;
又∵2+4=6,
∴log24,log216,log264存在怎样的关系式:log24+log216=log264;
(3)logaM+logaN=logaMN,
证明:∵am•an=am+n,
∴logaam•an=logaam+n=m+n,
∵logaam+logaan=m+n,
∴logaam+logaan=logaam•an,
设M=am,N=an,
则logaM+logaN=logaMN.
故答案是:(1)2;4;6;
(2)解:4×16=64;
log24+log216=log264;
logaMN
∴log24=2;log216=4;log264=6;
(2)解:4,16,64之间存在怎样的关系式:4×16=64;
又∵2+4=6,
∴log24,log216,log264存在怎样的关系式:log24+log216=log264;
(3)logaM+logaN=logaMN,
证明:∵am•an=am+n,
∴logaam•an=logaam+n=m+n,
∵logaam+logaan=m+n,
∴logaam+logaan=logaam•an,
设M=am,N=an,
则logaM+logaN=logaMN.
故答案是:(1)2;4;6;
(2)解:4×16=64;
log24+log216=log264;
logaMN
点评:本题考查了幂的运算,正确理解题目中给出的对数的定义是关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 记为
记为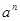 ,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为
,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为 (即
(即 =
= =3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为
=3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为 (即
(即 =n),如34=81,则4叫做以3为底81的对数,记为
=n),如34=81,则4叫做以3为底81的对数,记为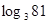 (即
(即 =4).
=4). 4= _____________________________ ;
4= _____________________________ ; M+
M+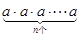 记为
记为 ,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为
,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为 (即
(即 =
= =3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为
=3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为 (即
(即 =n),如34=81,则4叫做以3为底81的对数,记为
=n),如34=81,则4叫做以3为底81的对数,记为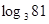 (即
(即 =4).
=4). 4= _____________________________ ;
4= _____________________________ ; M+
M+ 记为
记为 ,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为
,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为 (即
(即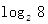 =
= =3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为
=3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为 (即
(即 =n),如34=81,则4叫做以3为底81的对数,记为
=n),如34=81,则4叫做以3为底81的对数,记为 (即
(即 =4).
=4). 4= _____________________________ ;
4= _____________________________ ; M+
M+