题目内容
 如图,若将边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,则图中阴影部分的面积为
如图,若将边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,则图中阴影部分的面积为1-
| ||
| 3 |
1-
.
| ||
| 3 |
分析:设B′C′与CD的交点为E,连接AE,利用“HL”证明Rt△AB′E和Rt△ADE全等,根据全等三角形对应角相等∠DAE=∠B′AE,再根据旋转角求出∠DAB′=60°,然后求出∠DAE=30°,再解直角三角形求出DE,然后根据阴影部分的面积=正方形ABCD的面积-四边形ADEB′的面积,列式计算即可得解.
解答: 解:如图,设B′C′与CD的交点为E,连接AE,
解:如图,设B′C′与CD的交点为E,连接AE,
在Rt△AB′E和Rt△ADE中,
,
∴Rt△AB′E≌Rt△ADE(HL),
∴∠DAE=∠B′AE,
∵旋转角为30°,
∴∠DAB′=60°,
∴∠DAE=
×60°=30°,
∴DE=1×
=
,
∴阴影部分的面积=1×1-2×(
×1×
)=1-
.
故答案为:1-
.
 解:如图,设B′C′与CD的交点为E,连接AE,
解:如图,设B′C′与CD的交点为E,连接AE,在Rt△AB′E和Rt△ADE中,
|
∴Rt△AB′E≌Rt△ADE(HL),
∴∠DAE=∠B′AE,
∵旋转角为30°,
∴∠DAB′=60°,
∴∠DAE=
| 1 |
| 2 |
∴DE=1×
| ||
| 3 |
| ||
| 3 |
∴阴影部分的面积=1×1-2×(
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
故答案为:1-
| ||
| 3 |
点评:本题考查了旋转的性质,正方形的性质,全等三角形判定与性质,解直角三角形,利用全等三角形求出∠DAE=∠B′AE,从而求出∠DAE=30°是解题的关键,也是本题的难点.

练习册系列答案
相关题目
 如图1,将边长为2cm的两个互相重合的正方形纸片按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为
如图1,将边长为2cm的两个互相重合的正方形纸片按住其中一个不动,另一个绕点B顺时针旋转一个角度,若使重叠部分的面积为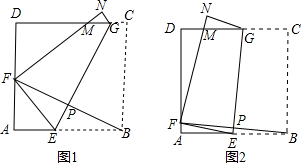 下一个正确结论(或结果):
下一个正确结论(或结果): 如图,若将边长为3和2的两小正方形纸板剪拼成一个大正方形,则该大正方形的边长为
如图,若将边长为3和2的两小正方形纸板剪拼成一个大正方形,则该大正方形的边长为