Question

利用二次函数的图象求下列方程的近似根．
（1）2x²-4x=5；       （2）x²+2x-10=3．

Answer 1

分析：画出抛物线y=2x²-4x-5与抛物线y=x²+2x-13的图象，观察它们的图象，再找出当函数值y=0时（即抛物线与x轴的交点）自变量x就是它们的解．

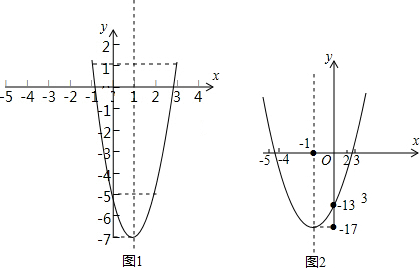
解答：解：（1）原方程变为：y=2x²-4x-5，画函数y=2x²-4x-5的图象．
列表：

x	-2	-1	0	1	2	3	4
y	11	1	-5	-7	-5	1	11

描点、连线，如图1所示．由图象知方程2x²-4x=5有两个根，一个在-1和0之间，另一个在2和3之间，先求-1和0之间的根，

x	-0.9	-0.8	-0.7
y	0.22	-0.52	-1.22

因此，x=-0.9是方程的近似根．
求2和3之间的根：

x	2.9	2.8	2.7
y	0.22	-0.52	-1.22

因此，x=2.9是方程的近似根．
综上所述，一元二次方程2x²-4x=5的解是x₁≈-0.9，x₂≈2.9．

（2）同（1），一元二次方程x²+2x-10=3解是x₁≈-4.8，x₂≈2.8．

点评：本题考查了图象法求一元二次方程的近似根．此题实际上是利用二次函数的图象解一元二次方程．