题目内容
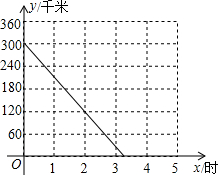 甲、乙两辆汽车同时从连接A、B两市的高速公路入口处分别驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变,甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.
甲、乙两辆汽车同时从连接A、B两市的高速公路入口处分别驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变,甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.(1)求y关于x的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,相遇前两车相距的路程为s(千米),请直接写出s关于x的表达式;
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即提高了a(千米/时)并保持匀速行驶,结果比预计提前一个小时到达终点,求乙车变化后的速度.在图中画出乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象.
考点:一次函数的应用
专题:
分析:(1)由图知y是x的一次函数,设y=kx+b.把图象经过的坐标代入求出k与b的值;
(2)根据路程与速度的关系列出方程可解;
(3)如图:当s=0时,x=2,即甲乙两车经过2小时相遇.再由1得出y=-90x+300.设y=0时,求出x的值可知乙车到达终点所用的时间.
(2)根据路程与速度的关系列出方程可解;
(3)如图:当s=0时,x=2,即甲乙两车经过2小时相遇.再由1得出y=-90x+300.设y=0时,求出x的值可知乙车到达终点所用的时间.
解答:解:(1)由图知,y是x的一次函数,设y=kx+b.
∵图象经过点(0,300)、(2,120),
∴
,
解得
.
∴y=-90x+300;
(2)s=-150x+300;
(3)在s=-150x+300中,当s=0时,x=2,即甲乙两车经过2小时相遇,此时乙车到达终点还有180千米的路程.
-
=1,解得a=30,即甲乙两车相遇后乙车速度为90千米/时.
乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象如图所示:

∵图象经过点(0,300)、(2,120),
∴
|
解得
|
∴y=-90x+300;
(2)s=-150x+300;
(3)在s=-150x+300中,当s=0时,x=2,即甲乙两车经过2小时相遇,此时乙车到达终点还有180千米的路程.
| 180 |
| 60 |
| 180 |
| 60+a |
乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象如图所示:

点评:此题考查一次函数图象求解析式.依次分析相遇问题,求相遇时间及速度,依据速度和时间画函数图象,重点考查学生的观察、理解及分析解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 将如图中的图形剪去一个正方形,使剩余的部分恰好能折成一个正方体,问应剪去哪个小正方形?(说出一种即可)
将如图中的图形剪去一个正方形,使剩余的部分恰好能折成一个正方体,问应剪去哪个小正方形?(说出一种即可)