题目内容
(1)阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值.对于任意正实数a、b,可作如下变形a+b=(
| a |
| b |
| a |
| b |
| ab |
| ab |
| a |
| b |
| ab |
又∵(
| a |
| b |
| a |
| b |
| ab |
| ab |
| ab |
根据上述内容,回答下列问题:在a+b≥2
| ab |
| p |
| p |
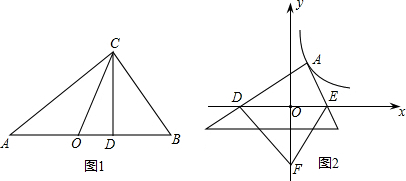
(2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a,DB=2b,试根据图形验证a+b≥2
| ab |
(3)探索应用:如图2,已知A为反比例函数y=
| 4 |
| x |
分析:(1)有给出的材料可知a=b时;
(2)因为AD=2a,DB=2b,所以AB=2a+2b,CO为中线,所以CO=a+b,再利用射影定理得CD=
=2
,在直角三角形COD中斜边大于直角边即CO>CD,问题得证;
(3)把A点的横坐标为1,代入函数y=
得,y=4,由(2)知:当DH=EH时,DE最小,此时S四边形ADFE=
×8×(4+3)=28.
(2)因为AD=2a,DB=2b,所以AB=2a+2b,CO为中线,所以CO=a+b,再利用射影定理得CD=
| AD•DB |
| ab |
(3)把A点的横坐标为1,代入函数y=
| 4 |
| x |
| 1 |
| 2 |
解答:解:(1)a=b
(2)由已知得CO=a+b,CD=2
,
CO≥CD,即a+b≥2
.
 当D与O重合时或a=b时,等式成立.
当D与O重合时或a=b时,等式成立.
(3)S四边形ADFE=S△ADE+S△FDE
=
DE•|yA|+
DE•OF=
DE(|yA|+OF),
当DE最小时S四边形ADFE最小.
过A作AH⊥x轴,由(2)知:当DH=EH时,DE最小,
在RT△ADE中,AH=
DE,
∴DE=2AH=2×4=8,
∴DE最小值为8,
此时S四边形ADFE=
×8×(4+3)=28.
(2)由已知得CO=a+b,CD=2
| ab |
CO≥CD,即a+b≥2
| ab |
 当D与O重合时或a=b时,等式成立.
当D与O重合时或a=b时,等式成立.(3)S四边形ADFE=S△ADE+S△FDE
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当DE最小时S四边形ADFE最小.
过A作AH⊥x轴,由(2)知:当DH=EH时,DE最小,
在RT△ADE中,AH=
| 1 |
| 2 |
∴DE=2AH=2×4=8,
∴DE最小值为8,
此时S四边形ADFE=
| 1 |
| 2 |
点评:本题考查了反比例函数的综合运用:利用图象解决问题,从图上获取有用的信息,是解题的关键所在.已知点在图象上,那么点一定满足这个函数解析式,反过来如果这点满足函数的解析式,那么这个点也一定在函数图象上.还能利用图象直接比较函数值或是自变量的大小.将数形结合在一起,是分析解决问题的一种好方法.

练习册系列答案
相关题目
 =
= -
- +
+ =
= +
+ ,
, ≥0,∴
≥0,∴ +
+ ≥0+
≥0+ ,即a+b≥
,即a+b≥ .
. (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,当且仅当a、b满足______时,a+b有最小值
,当且仅当a、b满足______时,a+b有最小值 .
. 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.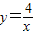 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
 =
= -
- +
+ =
=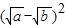 +
+ ,
, ≥0,∴
≥0,∴ +
+ ≥0+
≥0+ ,即a+b≥
,即a+b≥ .
. (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,当且仅当a、b满足______时,a+b有最小值
,当且仅当a、b满足______时,a+b有最小值 .
. 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件. 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
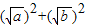 =
=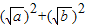 -
-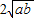 +
+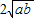 =
=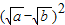 +
+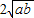 ,
,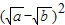 ≥0,∴
≥0,∴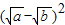 +
+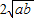 ≥0+
≥0+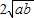 ,即a+b≥
,即a+b≥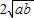 .
.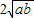 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥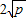 ,当且仅当a、b满足______时,a+b有最小值
,当且仅当a、b满足______时,a+b有最小值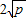 .
.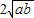 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.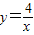 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
 =
= -
- +
+ =
=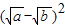 +
+ ,
, ≥0,∴
≥0,∴ +
+ ≥0+
≥0+ ,即a+b≥
,即a+b≥ .
. (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥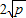 ,当且仅当a、b满足______时,a+b有最小值
,当且仅当a、b满足______时,a+b有最小值 .
. 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件. 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.