题目内容
四边形ABCD中,∠A比∠B大40°,∠C比∠B小10°,∠D=30°,求∠A、∠B、∠C的 度数.
度数.
解:设∠B=x,则∠A=________,∠C=________,
根据四边形内角和为________°得:
________
解得x=________
所以∠B=________,∠A=________,∠C=________.
答:________.
x+40° x-10° 360° x+(x+40°)+(x-10°)+30°=360° 100° 100° 140° 90° ∠B=100°,∠A=140°,∠C=90°
分析:根据题目中已知的相等关系,就可以已知一个量时,表示出另外的量.根据四边形的内角和是360度,列出方程求解即可.
解答:设∠B=x,则∠A=x+40°,∠C=x-10°,
根据四边形内角和为360°得:
x+(x+40°)+(x-10°)+30°=360°,
解得x=100°.
所以∠B=100°,∠A=140°,∠C=90度.
答:∠B=100°,∠A=140°,∠C=90度.
点评:正确理解题目中各量之间的相等关系是解题的关键,列方程的重点是找出相等关系.
分析:根据题目中已知的相等关系,就可以已知一个量时,表示出另外的量.根据四边形的内角和是360度,列出方程求解即可.
解答:设∠B=x,则∠A=x+40°,∠C=x-10°,
根据四边形内角和为360°得:
x+(x+40°)+(x-10°)+30°=360°,
解得x=100°.
所以∠B=100°,∠A=140°,∠C=90度.
答:∠B=100°,∠A=140°,∠C=90度.
点评:正确理解题目中各量之间的相等关系是解题的关键,列方程的重点是找出相等关系.

练习册系列答案
相关题目
 23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.
23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.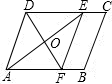 如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )
如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( ) 17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形:
17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形: 7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.
7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.