Question

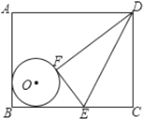
【题目】如图，△ABC是等腰直角三角形，AC=BC=2，以斜边AB上的点O为圆心的圆分别与AC、BC相切于点D、E，与AB分别相交于点G、H，且DG的延长线与CB的延长线交于点F，分析下列四个结论：①HG=2；②BG=BF；③AH=BG=；④CF= .其中正确的结论个数有( )

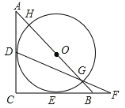
A.1个B.2个C.3个D.4个

Answer 1

【答案】D

【解析】

如右图所示，连接OD、OE，根据切线的性质得到∠ODC=∠OEC=90°，OE=OD，据等腰直角三角形的性质得到∠C=90°，∠A=45°，得到四边形DCEO是正方形，求得OD=AD=AC=1，于是得到HG=2OD=2；故①正确；求得∠EOB=45°，得到∠ODG=135°，得到∠OGD=∠ODG=22.5°，根据等腰三角形的性质得到BG=BF，故②正确；根据角平分线的判定定理得到O在∠ACB的角平分线上，根据等腰三角形的性质得到O是AB中点，求得AD=CD=OD=OE=1，得到OG=1，根据勾股定理得到AB=

AC=，于是得到AH=BG=，故③正确；CF=2+BF=．故④正确．

如右图所示，连接OD、OE，

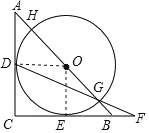
∵⊙O与AC、BC切于点D. E，

∴∠ODC=∠OEC=90°，OE=OD，

又∵△ABC是等腰直角三角形，

∴∠C=90°,∠A=45°，

∴四边形DCEO是正方形，

∴OD∥BC，OE=OD，OD⊥AC，

△ADO是等腰直角三角形，

∴OD=AD=AC=1，

∴HG=2OD=2；故①正确；

∵AC=BC,∴∠A=∠ABC=45°，

∴∠EOB=45°，

∴∠ODG=135°，

∵OD=OG，

∴∠OGD=∠ODG=22.5°，

∴∠BGF=22.5°，

∵∠BGF+∠F=∠ABC=45°，

∴∠F=22.5°，

∴BG=BF，故②正确；

∵OE=OD，

∴O在∠ACB的角平分线上，

∴O是AB中点，

∴AD=CD，

又∵AC=2，

∴AD=CD=OD=OE=1，

∴OG=1，

又∵ABAC=，

∴OB=，

∴BG=OBOG=，

同理AH=BG=，故③正确；

∴CF=2+BF=.故④正确。

故选D.