题目内容
)如图13,已知Rt△ACB中,∠C=90°,∠BAC=45°.
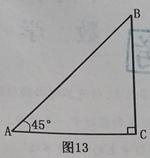
(1)(4分)用尺规作图,:在CA的延长线上截取AD=AB,并连接
BD(不写作法,保留作图痕迹)
(2)(4分)求∠BDC的度数.
(3)(4分)定义:在直角三角形中,一个锐角A的邻边与对边的比叫
做∠A的余切,记作cotA,即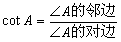 ,根据定义,利
,根据定义,利
用图形求cot22.5°的值.
、解:(1)如图,

(2)∵AD=AB,
∴∠ADB=∠ABD,
而∠BAC=∠ADB+∠ABD,
∴∠ADB =
= ∠BAC=
∠BAC= ×45°=22.5°,
×45°=22.5°,
即∠BDC的度数为22.5°;
(3)设AC=x,
∵∠C=90°,∠BAC=45°,
∴△ACB为等腰直角三角形,
∴BC=AC=x,AB= AC=
AC= x,
x,
∴AD=AB= x,
x,
∴CD= x+x=(
x+x=( +1)x,
+1)x,
在Rt△BCD中,cot∠BDC= =
= =
= +1,
+1,
即cot22.5°= +1.
+1.

练习册系列答案
相关题目
 B.
B.  C.
C.  D.
D. 
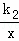 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.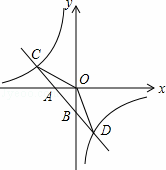
 的一个根,则方程的另一个根x2是 m(m-n)2
的一个根,则方程的另一个根x2是 m(m-n)2
 ;②
;② ;③
;③ ;④
;④ ,其中做对的一道题的序号是
,其中做对的一道题的序号是 =
=  D=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是 (结果不取近似值).
D=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是 (结果不取近似值).