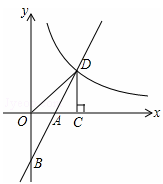
题目内容

在直角坐标系中，设x轴为直线l，函数的图像分别是，半径为1的与直线中的两条相切，例如是其中一个的圆心坐标.
（1）写出其余满足条件的的圆心坐标；
（2）在图中标出所有圆心，并用线段依次连接各圆心，求所得几何图形的周长.

（1）；（2）.

解析试题分析：（1）根据的圆心所在的直线和轴对称性求解.
（2）依次连接各圆心，所得几何图形的边长相等，从而求得所得几何图形的周长.
试题解析：（1）分两类，利用对称求解：
①的圆心在相邻直线对称轴和y轴上时，

②的圆心在不相邻直线对称轴和x轴上时，

（2）如图，依次连接各圆心，所得几何图形的边长相等，为，
∴所得几何图形的周长为.

考点：1.一次函数的图象；2.直线与圆的位置关系；3.直线上点的坐标与方程的关系；4.轴对称的性质.

练习册系列答案
相关题目

某办公用品销售商店推出两种优惠方法：①购1个书包，赠送1支水性笔；②购书包和水性笔一律按9折优惠．书包每个定价20元，水性笔每支定价5元．小丽和同学需买4个书包，水性笔若干支（不少于4支）．
（1）分别写出两种优惠方法购买费用y（元）与所买水性笔支数x（支）之间的函数关系式；
（2）对x的取值情况进行分析，说明按哪种优惠方法购买比较便宜；
（3）小丽和同学需买这种书包4个和水性笔12支，请你设计怎样购买最经济．

如图，这是反映爷爷每天晚饭后从家中出发去元宝山公园锻炼的时间与距离之间关系的一幅图．

(1)右图反映的自变量、因变量分别是什么？
(2)爷爷每天从公园返回用多长时间？
(3)爷爷散步时最远离家多少米？
(4)爷爷在公园锻炼多长时间？
(5)计算爷爷离家后的2 0分钟内的平均速度．

为了响应国家节能减排的号召，鼓励市民节约用电，我市从2012年7月1日起，居民用电实行“一户一表”的“阶梯电价”，分三个档次收费，第一档是用电量不超过180千瓦时实行“基本电价”，第二、三档实行“提高电价”，具体收费情况如图的折线图，请根据图象回答下列问题；
(1)当用电量是180千瓦时时，电费是__________元；
(2)第二档的用电量范围是__________；
(3)“基本电价”是__________元/千瓦时；
(4)小明家8月份的电费是328．5元，这个月他家用电多少千瓦时？

已知直线经过点(1，－1)，求关于x的不等式2x－b≥0的解集.

如图，在平面直角坐标系中，直线y＝2x＋b（b＜0）与坐标轴交于A，B两点，与双曲线（x>0）交于D点，过点D作DC⊥x轴，垂足为C，连接OD。已知△AOB≌△ACD。
（1）如果b=－2，求k的值；
（2）试探究k与b的数量关系，并写出直线OD的解析式。

已知A、B两地相距300千米，甲、乙两车同时从A地出发，以各自的速度匀速往返两地，甲车先到达B地，停留1小时后按原路返回．设两车行驶的时间为x小时，离开A地的距离是y千米，如图是y与x的函数图象．
(1)计算甲车的速度为   千米／时，乙车的速度为   千米／时；
(2)几小时后两车相遇；
(3)在从开始出发到两车相遇的过程中，设两车之间的距离为S千米，乙车行驶的时间为t小时，求S与t之间的函数关系式．

在学习三角形中线的知识时，小明了解到：三角形的任意一条中线所在的直线可以把该三角形分为面积相等的两部分。进而，小明继续研究，过四边形的某一顶点的直线能否将该四边形平分为面积相等的两部分？他画出了如下示意图（如图1），得到了符合要求的直线AF.

小明的作图步骤如下：
第一步：连结AC；
第二步：过点B作BE//AC交DC的延长线于点E；
第三步：取ED中点F，作直线AF；
则直线AF即为所求.
请参考小明思考问题的方法，解决问题：
如图2，五边形ABOCD，各顶点坐标为：A(3,4)，B(0,2)，O(0,0)，C(4,0)，D(4,2).请你构造一条经过顶点A的直线，将五边形ABOCD分为面积相等的两部分，并求出该直线的解析式.

已知一次函数y=ｋx+ｂ的图象经过点A（０，－１），B（１，０），求这个一次函数的表达式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网