Question

如图所示，在凸四边形ABCD中，∠ABD＞∠CBD，∠ADB＞∠CDB．求证：AB+AD＞BC+CD．

Answer 1

分析：如图，过顶点B作∠EBD=∠CBD，BE=BC，连接ED，延长BE交AD于点F．构造全等三角形：△BCD≌△BED（SAS），则对应边ED=CD，故根据三角形三边关系得到：AB+AD=AB+AF+FD＞BF+FD=BE+EF+FD＞BE+ED，即AB+AD＞BC+CD．

解答：证明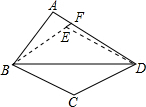：∵∠ABD＞∠CBD，∠ADB＞∠CDB，
∴如图，过顶点B作∠EBD=∠CBD，BE=BC，连接ED，延长BE交AD于点F．
∵在△BCD与△BED中，

BE=BC ∠EBD=∠CBD BD=BD

，
∴△BCD≌△BED（SAS），
∴ED=CD，
∴AB+AD=AB+AF+FD＞BF+FD=BE+EF+FD＞BE+ED，即AB+AD＞BC+CD．

点评：本题考查了全等三角形的判定与性质、三角形的三边关系．在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．