题目内容

精英家教网图①是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称抽）剪开，把它分成四块形状和大小都一样的小长方形，然后按图②那样拼成一个正方形，则中间空的都分的面积是（　　）
A、abB、a2+2ab+b2C、a2-b2D、a2-2ab+b2
分析：先求出正方形的边长，继而得出面积，然后根据空白部分的面积=正方形的面积-矩形的面积即可得出答案．
解答：解：图（1）是一个长为2a，宽为2b（a＞b）的长方形，
∴正方形的边长为：a+b，
∴正方形的面积为（a+b）2，
∵原矩形的面积为4ab，
∴中间空的部分的面积=（a+b）2-4ab=a2-2ab+b2．
故选：D．
点评：此题考查了完全平方公式的几何背景，求出正方形的边长是解答本题的关键．
练习册系列答案
相关题目
24、如图1是一个长为2a、宽为2b的长方形，沿图中虚线用剪刀均匀分成四块小长方形，然后按图2形状拼成一个正方形．
（1）图2中的空白部分的正方形的边长是多少？（用含a、b的式子表示）
（2）已知a+b=7，ab=6，求图2中空白部分的正方形的面积．
（3）观察图2，用一个等式表示下列三个整式：（a+b）2，（a-b）2，ab之间的数量关系．
图1是一个长为2a，宽为2b的长方形，沿图中虚线剪开，可分成四块小长方形．
（1）你认为图1的长方形面积等于
4ab
4ab
；
（2）将四块小长方形拼成一个图2的正方形．请用两种不同的方法求图2中 阴影部分的面积．           
方法1：
（a+b）2-4ab
（a+b）2-4ab
；方法2：
（a-b）2
（a-b）2
；
（3）观察图2直接写出代数式（a+b）2、（a-b）2、ab之间的等量关系
（a+b）2-4ab=（a-b）2
（a+b）2-4ab=（a-b）2
；
（4）把四块小长方形不重叠地放在一个长方形的内部（如图3），未被覆盖的部分用阴影表示．求两块阴影部分的周长和（用含m、n的代数式表示）．
图1是一个长为2a，宽为2b的长方形，沿图中虚线剪开，可分成四块小长方形．
（1）求出图1的长方形面积；
（2）将四块小长方形拼成一个图2的正方形．利用阴影部分面积的不同表示方法，直接写出代数式（a+b）2、（a-b）2、ab之间的等量关系；
（3）把四块小长方形不重叠地放在一个长方形的内部（如图3），未被覆盖的部分用阴影表示．求两块阴影部分的周长和（用含m、n的代数式表示）．
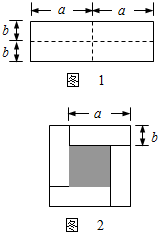如图1是一个长为2a，宽为2b的长方形，沿图中虚线剪开分成四块小长方形，然后按如图2的形状拼成一个正方形．
（1）图2的阴影部分的正方形的边长是
a-b
a-b
．
（2）用两种不同的方法求图中阴影部分的面积．
【方法1】S阴影=
（a-b）2
（a-b）2
；
【方法2】S阴影=
（a+b）2-4ab
（a+b）2-4ab
；
（3）观察如图2，写出（a+b）2，（a-b）2，ab这三个代数式之间的等量关系．
（4）根据（3）题中的等量关系，解决问题：
若x+y=10，xy=16，求x-y的值．
如图1是一个长为2a、宽为2b的长方形，沿图中虚线用剪刀均匀分成四块小长方形，然后按图2形状拼成一个正方形．
（1）图2中的空白部分的正方形的边长是多少？（用含a、b的式子表示）
（2）已知a+b=7，ab=6，求图2中空白部分的正方形的面积．
（3）观察图2，用一个等式表示下列三个整式：（a+b）2，（a﹣b）2，ab之间的数量关系．
                                                  
                                                   图1                                                图2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网