Question

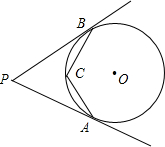
如图，PA、PB分别切⊙O于A、B，连接PO、AB相交于D，C是⊙O上一点，∠C=60°。
（1）求∠APB的大小；
（2）若PO=20cm，求△AOB的面积。

Answer 1

解：（1）∵PA、PB分别切⊙O于A、B，∴OA⊥PA，OB⊥PB。∴∠PAO=∠PBO=90°。
∵∠C=60°，∴∠AOB=2∠C=2×60°=120°。
∴∠APB=360°－∠PAO－∠PBO－∠AOB=60°。
（2）∵PA、PB分别切⊙O于A、B，∴∠APO=∠APB=×60°=30°，PA=PB。
∴P在AB的垂直平分线上。
∵OA=OB，∴O在AB的垂直平分线上，即OP是AB的垂直平分线，
∴OD⊥AB，AD=BD=AB。
∵∠PAO=90°，∴∠AOP=60°。
在Rt△PAO中，AO=PO=×20=10，
在Rt△AOD中，AD=AO•sin60°=10×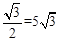，OD=OA•cos60°=10×=5，
∴AB=2AD=，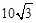
∴△AOB的面积为：AB•OD=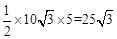（cm²）。

解析