题目内容
【题目】已知一副三角板按如图1方式拼接在一起，其中边
，
与直线
重合，
，
．
（1）图 1 中，
=______°．
（2）如图2，三角板
固定不动，将三角板
绕点
按顺时针方向旋转一个角度
，在转动过程中两块三角板都在直线的上方：
①当
平分、、
其中的两边组成的角时，求满足要求的所有旋转角度的值；
②是否存在
？若存在，求此时的的值；若不存在，请说明理由．
【答案】（1）75；（2）①旋转角度
的值为
，
，
；②当
或
时，存在
.
【解析】
（1）根据平角的定义即可求出
；
（2）①根据OB所平分的角分类讨论，分别求出旋转角度即可；
②根据OA和OD的相对位置分类讨论，分别求出旋转角度即可．
解：（1）
，
．
故答案为：
；
（2）①当
平分
时．
∵平分
当平分
时．
，
∴
；
当平分
时．
，
，
，
综上所述：旋转角度的值为，，；
②当
在
的左侧时，则
，
，
；
当在的右侧时，则
，
．
，
，
，
综上所述：当或时，存在．
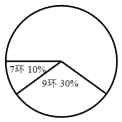
名校课堂系列答案【题目】在全运会射击比赛的选拔赛中，运动员甲10次射击成绩的统计表和扇形统计图如下：
命中环数 | 10 | 9 | 8 | 7 |
命中次数 | 3 | 2 |
（1）根据统计表（图）中提供的信息，补全统计表及扇形统计图；
（2）已知乙运动员10次射击的平均成绩为9环，方差为1．2，如果只能选一人参加比赛，你认为应该派谁去？并说明理由．
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 59 | 96 | 116 | 290 | 480 | 601 |
摸到白球的频率 |
| 0.64 | 0.58 |
| 0.60 | 0.601 |
（1）完成上表；
（2）“摸到白球”的概率的估计值是 （精确到0.1）；
（3）试估算口袋中黑、白两种颜色的球各有多少只？
