Question

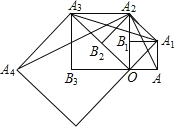
【题目】如图，四边形 OAA1B1 是边长为 1 的正方形，以对角线 OA1 为边作第二个正方形 OA1A2B2，连接 AA2，得到△ AA1A2；再以对角线 OA2 为边作第三个正方形 OA2A3B3，连接 A1A3，得到△A1A2A3；再以对角线 OA3 为边作第 四个正方形，连接 A2A4，得到△A2A3A4……记△AA1A2、△A1A2A3、△A2A3A4 的面积分别为 S1、S2、S3，如此下 去，则 S2019＝_____ ．

Answer 1

【答案】

【解析】

根据正方形的性质，边长都相等，求出△ AA1A2的面积，利用勾股定理求得，求出，以此类推即可得出．

解：∵四边形是正方形，

∴，∴，

∵，∴，

∴，∴，

同理可求：，

，

∴，

∴，

故答案为：．