题目内容
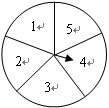
如图,一个圆形转盘被等分成五个扇形区域,上面分别标有数字1、2、3、4、5,转盘指针的位置固定,转动转盘后任其自由停止.转动转盘一次,当转盘停止转动时,记指针指向标有偶数所在区域的概率为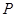 (偶数),指针指向标有奇数所在区域的概率为
(偶数),指针指向标有奇数所在区域的概率为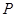 (奇数),则
(奇数),则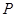 (偶数)
(偶数) 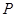 (奇数)(填“
(奇数)(填“ ”“
”“ ”或“
”或“ ”).
”).
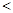
解析考点:几何概率.
分析:根据题意分别求出奇数和偶数在整个圆形转盘中所占的比例,再进行比较即可.
解:∵一个圆形转盘被等分成五个扇形区域,有2个偶数区,3个奇数区,
∴有p(偶数)=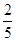 ,p(奇数)=
,p(奇数)=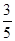 ,所以p(偶数)<p(奇数).
,所以p(偶数)<p(奇数).
故答案为: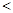

练习册系列答案
相关题目
如图,一个圆形转盘被等分成七个扇形区域,上面分别标有数字1、2、3、4、5、6、7,转盘指针的位置固定,转动转盘后自由停止.转动转盘一次,当转盘停止转到时,记指针指向标有偶数所在区域的概率为P(偶数),指针指向标有奇数所有区 域的概率为P(奇数),则P(偶数)与P(奇数)的大小关系是( )
域的概率为P(奇数),则P(偶数)与P(奇数)的大小关系是( )
 域的概率为P(奇数),则P(偶数)与P(奇数)的大小关系是( )
域的概率为P(奇数),则P(偶数)与P(奇数)的大小关系是( )| A、P(偶数)>P(奇数) | B、P(偶数)=P(奇数) | C、P(偶数)<P(奇数) | D、P(偶数)≤P(奇数) |
 如图,一个圆形转盘被等分成五个扇形区域,上面分别标有数字1,2,3,4,5,转盘指针的位置固定,转动转盘后任其自由停止.转动转盘一次,当转盘停止转动时,记指针指向标有偶数所在区域的概率为P(偶数),指针指向标有奇数所在区域的概率为P(奇数),则P(偶数)
如图,一个圆形转盘被等分成五个扇形区域,上面分别标有数字1,2,3,4,5,转盘指针的位置固定,转动转盘后任其自由停止.转动转盘一次,当转盘停止转动时,记指针指向标有偶数所在区域的概率为P(偶数),指针指向标有奇数所在区域的概率为P(奇数),则P(偶数) 15、如图,一个圆形转盘被等分成八个扇形区域,上面分别标有数字1、2、3、4,转盘指针的位置固定,转动转盘后任其自由停止.转动转盘一次,当转盘停止转动时,记指针指向标有“3”所在区域的概率为P(3),指针指向标有“4”所在区域的概率为P(4),则P(3)
15、如图,一个圆形转盘被等分成八个扇形区域,上面分别标有数字1、2、3、4,转盘指针的位置固定,转动转盘后任其自由停止.转动转盘一次,当转盘停止转动时,记指针指向标有“3”所在区域的概率为P(3),指针指向标有“4”所在区域的概率为P(4),则P(3) 如图,一个圆形转盘被等分成八个扇形区域,上面分别标上1,3,4,5,6,7,8,9,转盘可以自由转动,转动转盘一次,指针指向的数字为偶数所在区域的概率是( )
如图,一个圆形转盘被等分成八个扇形区域,上面分别标上1,3,4,5,6,7,8,9,转盘可以自由转动,转动转盘一次,指针指向的数字为偶数所在区域的概率是( )