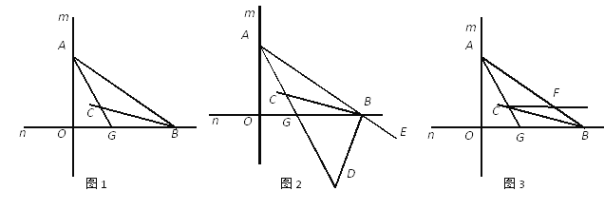
题目内容
【题目】已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一点,且
边上一点,且![]() ,
,![]() 为
为![]() 边的中点,连接
边的中点,连接![]() ,设
,设![]()
(1)当![]() 时(如图),连接
时(如图),连接![]() ,则
,则![]() 的长为___________;
的长为___________;
(2)设![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,以
,以![]() 为圆心
为圆心![]() 为半径作
为半径作![]() ,试问:当
,试问:当![]() 的长改变时,点
的长改变时,点![]() 与
与![]() 的位置关系变化吗?若不变化,请说明具体的位置关系,并证明你的结论;若变化,请说明理由.
的位置关系变化吗?若不变化,请说明具体的位置关系,并证明你的结论;若变化,请说明理由.

【答案】(1)4;(2)![]() (3)点
(3)点![]() 在
在![]() 上
上
【解析】
(1)利用已知条件即可得到DE是线段BC的垂直平分线,根据垂直平分线的性质即可得到BD的长;
(2)分别表示出两个三角形的面积,利用它们的面积的比即可得到函数关系式;
(3)由已知条件得出AP=AM之后即可得到点与圆的位置关系.
(1)如图所示,连接![]() .
.

![]() ,
,![]() 为
为![]() 边的中点,
边的中点,
![]() ;
;
(2)![]() 为
为![]() 边的中点,
边的中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
![]() .
.
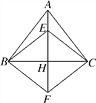
(3)点![]() 在
在![]() 上,理由如下:
上,理由如下:
如图所示,取![]() 中点
中点![]() ,则
,则![]() ;
;

![]() 为
为![]() 中点,
中点,
![]()
![]() 为
为![]() 中点,
中点,
![]() 且
且![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() 点
点![]() 在
在![]() 上.
上.

练习册系列答案
相关题目