题目内容
如图(1),点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P,Q出发t秒时,△BPQ的面积为ycm,已知y与t的函数关系的图形如图(2)(曲线OM为抛物线的一部分),则下列结论:
①AD=BE=5cm;②当0<t≤5时,y=
t2;③直线NH的解析式为y=-
t+27;④若△ABE与△QBP相似,则t=
秒.
其中正确的结论为 .

①AD=BE=5cm;②当0<t≤5时,y=
| 2 |
| 5 |
| 5 |
| 2 |
| 29 |
| 4 |
其中正确的结论为

考点:动点问题的函数图象
专题:
分析:据图(2)可以判断三角形的面积变化分为三段,可以判断出当点P到达点E时点Q到达点C,从而得到BC、BE的长度,再根据M、N是从5秒到7秒,可得ED的长度,然后表示出AE的长度,根据勾股定理求出AB的长度,然后针对各小题分析解答即可.
解答:解:①根据图(2)可得,当点P到达点E时点Q到达点C,
∵点P、Q的运动的速度都是1cm/s,
∴BC=BE=5cm,
∴AD=BE=5(故①正确);
②如图1,过点P作PF⊥BC于点F,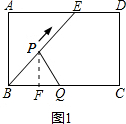
根据面积不变时△BPQ的面积为10,可得AB=4,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB=
=
,
∴PF=PBsin∠PBF=
t,
∴当0<t≤5时,y=
BQ•PF=
t•
t=
t2(故②正确);
③根据5-7秒面积不变,可得ED=2,
当点P运动到点C时,面积变为0,此时点P走过的路程为BE+ED+DC=11,
故点H的坐标为(11,0),
设直线NH的解析式为y=kx+b,
将点H(11,0),点N(7,10)代入可得:
,
解得:
.
故直线NH的解析式为:y=-
t+
,(故③错误);
④当△ABE与△QBP相似时,点P在DC上,如图2所示:
∵tan∠PBQ=tan∠ABE=
,
∴
=
,即
=
,
解得:t=
.(故④正确);
综上可得①②④正确.
故答案为:①②④.
∵点P、Q的运动的速度都是1cm/s,
∴BC=BE=5cm,
∴AD=BE=5(故①正确);
②如图1,过点P作PF⊥BC于点F,

根据面积不变时△BPQ的面积为10,可得AB=4,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB=
| AB |
| BE |
| 4 |
| 5 |
∴PF=PBsin∠PBF=
| 4 |
| 5 |
∴当0<t≤5时,y=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
③根据5-7秒面积不变,可得ED=2,
当点P运动到点C时,面积变为0,此时点P走过的路程为BE+ED+DC=11,
故点H的坐标为(11,0),
设直线NH的解析式为y=kx+b,
将点H(11,0),点N(7,10)代入可得:
|
解得:
|
故直线NH的解析式为:y=-
| 5 |
| 2 |
| 55 |
| 2 |
④当△ABE与△QBP相似时,点P在DC上,如图2所示:

∵tan∠PBQ=tan∠ABE=
| 3 |
| 4 |
∴
| PQ |
| BQ |
| 3 |
| 4 |
| 11-t |
| 5 |
| 3 |
| 4 |
解得:t=
| 29 |
| 4 |
综上可得①②④正确.
故答案为:①②④.
点评:本题考查了二次函数的综合应用及动点问题的函数图象,根据图(2)判断出点P到达点E时,点Q到达点C是解题的关键,也是本题的突破口,难度较大.

练习册系列答案
相关题目
计算:
(1)7x+4(x2-2)-2(2x2-x+3);
(2)4ab-3b2-[(a2+b2)-(a2-b2)];
(3)(3mn-5m2)-(3m2-5mn);
(4)2a+2(a+1)-3(a-1).
(1)7x+4(x2-2)-2(2x2-x+3);
(2)4ab-3b2-[(a2+b2)-(a2-b2)];
(3)(3mn-5m2)-(3m2-5mn);
(4)2a+2(a+1)-3(a-1).
下列说法正确的是( )
| A、若a≠b,则a2≠b2 |
| B、零除以任何数都等于零 |
| C、任何负数都小于它的相反数 |
| D、两个负数比较大小,绝对值大的就大 |
 如图,在△ABC中,AB=AC,∠BAC=90°,分别从点B、C向过A点的直线作垂线,垂足为M、N,若BM=4,AC=5,求线段MN的长.
如图,在△ABC中,AB=AC,∠BAC=90°,分别从点B、C向过A点的直线作垂线,垂足为M、N,若BM=4,AC=5,求线段MN的长.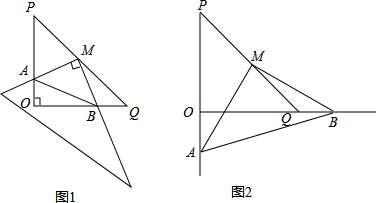

 请把+(-3),(-2)2,-|-2.5|,0,-(-1.5)这五个数先化简,再将化简结果按从小到大顺序,从左到右串个糖葫芦,把数填在“○”内.
请把+(-3),(-2)2,-|-2.5|,0,-(-1.5)这五个数先化简,再将化简结果按从小到大顺序,从左到右串个糖葫芦,把数填在“○”内.