题目内容
矩形ABCD中，E是CD上一点，CE：ED=1：3，AD：AE=1：2，则△ABE为
- A.锐角三角形
- B.直角三角形
- C.钝角三角形
- D.等腰三角形
B
分析：先依题意作出简单的图形，再依据勾股定理逆定理得出AB2=AE2+BE2，即可得出其为直角三角形．
解答：
解：如图，
在Rt△ADE中，∵AD：AE=1：2，
∴∠AED=30°，
DE=
AD，又CE：ED=1：3，
∴CE=
DE=
BC，CD=
BC．
AE2=AD2+DE2=4AD2，BE2=
BC2，AB2=CD2=
BC2．
∵AB2=AE2+BE2=BC2，
∴AE⊥BE，即△ABE是直角三角形．
故选B．
点评：本题主要考查了简单的直角三角形的求解问题，能够熟练掌握．
分析：先依题意作出简单的图形，再依据勾股定理逆定理得出AB2=AE2+BE2，即可得出其为直角三角形．
解答：
解：如图，在Rt△ADE中，∵AD：AE=1：2，
∴∠AED=30°，
DE=
AD，又CE：ED=1：3，∴CE=
DE=BC，CD=BC．AE2=AD2+DE2=4AD2，BE2=
BC2，AB2=CD2=BC2．∵AB2=AE2+BE2=
BC2，∴AE⊥BE，即△ABE是直角三角形．
故选B．
点评：本题主要考查了简单的直角三角形的求解问题，能够熟练掌握．
练习册系列答案
相关题目
（2012•溧水县二模）如图，矩形ABCD中，E是CD的中点，∠DAE=15°，则cos∠AEB=
如图，在矩形ABCD中，E是BC边上的点，AE=BC，DF⊥AE，垂足为F，连接DE．证明：AB=DF．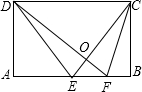
如图：矩形ABCD中，E是AB的中点，2AD=AB，F是BE的中点．若AD=5，那么△OCD的面积是
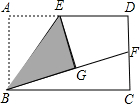（2012•成都模拟）如图，在矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，且点G在矩形ABCD内部，再延长BG交DC于点F．