题目内容
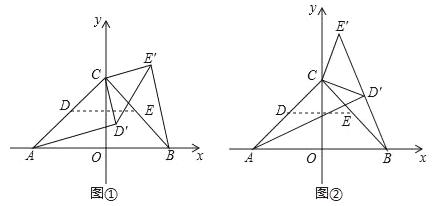
在平面直角坐标系中,点 A(﹣2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.
(1)如图①,若 0°<α<90°,当 AD′∥CE′时,求α的大小;
(2)如图②,若 90°<α<180°,当点 D′落在线段 BE′上时,求 sin∠CBE′的值;
(3)若直线AD′与直线BE′相交于点P,求点P的横坐标m的取值范围(直接写出结果即可).
练习册系列答案
相关题目
下表给出了代数式﹣x2+bx+c与x的一些对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
﹣x2+bx+c | … | 5 | n | c | 2 | ﹣3 | ﹣10 | … |
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=﹣x2+bx+c,直接写出0≤x≤2时y的最大值.


 的图象在第一、三象限的概率是_____.
的图象在第一、三象限的概率是_____.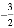 B. ﹣1 C.
B. ﹣1 C. 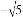 D. 0
D. 0