题目内容
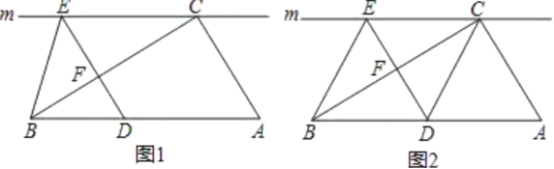
【题目】如图,矩形![]() 的对角线交于点
的对角线交于点![]() ,点
,点![]() 是矩形外的一点,其中
是矩形外的一点,其中![]() 。
。
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,连接
,连接![]() 交于
交于![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() 平分
平分![]() 。
。

【答案】(1)见解析;(2)见解析.
【解析】
(1)由矩形可知OA=OB,由AE∥BD,BE∥AC,即可得出结论;
(2)利用矩形和菱形的性质先证△COF≌△EBF,得到OF=BF,再求得∠AOB=60°,利用有一个角是60°的等腰三角形是等边三角形,得到△AOB为等边三角形,最后利用三线合一的性质得到AF平分∠BAO.
证明:(1)∵四边形![]() 是矩形,
是矩形,
∴![]() 则
则![]() ,
,
即∴![]()
又∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴四边形![]() 是菱形;
是菱形;
(2)∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中

∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∵![]() ,
,
∴![]() 平分
平分![]() .
.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目