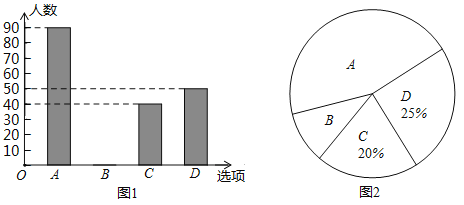
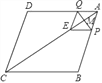
题目内容
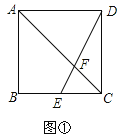
【题目】如图,点E是矩形ABCD的边BC的中点,连接DE交AC于点F.
![]() 如图
如图![]() ,求证:
,求证:![]() ;
;
![]() 如图
如图![]() ,作
,作![]() 于G,试探究:当AB与AD满足什么关系时,使得
于G,试探究:当AB与AD满足什么关系时,使得![]() 成立?并证明你的结论;
成立?并证明你的结论;
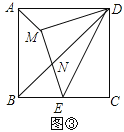
![]() 如图
如图![]() ,以DE为斜边在矩形ABCD内部作等腰
,以DE为斜边在矩形ABCD内部作等腰![]() ,交对角线BD于N,连接AM,若
,交对角线BD于N,连接AM,若![]() ,请直接写出
,请直接写出![]() 的值.
的值.

【答案】(1)证明见解析;(2)结论:当![]() 时,
时,![]() 成立;(3)
成立;(3)![]() .
.
【解析】分析:(1)、根据中点的性质得出AD=BC=2CE,然后根据平行线的性质得出答案;(2)、设BE=EC=a,从而得出DE的长度,然后根据平行线的性质得出DF=2a=AD,根据垂直从而得出答案;(3)、过M作GF⊥AD,交AD于G,交BC于F,从而得出![]() 和
和![]() 全等,然后根据题意得出
全等,然后根据题意得出![]() 和
和![]() 相似,根据相似三角形的相似比得出答案.
相似,根据相似三角形的相似比得出答案.
详解:![]() 证明:
证明:![]() 点E是矩形ABCD的边BC的中点,
点E是矩形ABCD的边BC的中点, ![]() ,
,
![]() 在矩形ABCD中,
在矩形ABCD中,![]() ,
, ![]() ,
, ![]() .
.
![]() 结论:当
结论:当![]() 时,
时,![]() 成立.
成立.
设![]() ,则
,则![]() ,
,![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
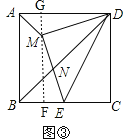
![]() 如图
如图![]() ,过M作
,过M作![]() ,交AD于G,交BC于F,
,交AD于G,交BC于F,
![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,
,
![]() ,
,![]() ,
, ![]() ,
,
在![]() 和
和![]() 中,
中,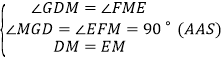 ,
, ![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
, ![]() ∽
∽![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() , 即
, 即![]() 的值是
的值是![]() .
.

练习册系列答案
相关题目