Question

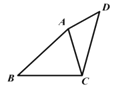
【题目】如图，在四边形 ABCD 中，AC 是对角线，AB=CD，∠DAC+∠BCA=180°，∠BAC+∠ACD=90°，四边形 ABCD 的面积是 18，则 CD 的长是__________.

Answer 1

【答案】6.

【解析】分析: 延长BC至点E,使CE=AD,再连接AE, 证△ACD≌△CAE得,再证△BAE是等腰直角三角形,得,最后根据即可求出CD的长.

详解:如图,延长BC至点E,使CE=AD,再连接AE.

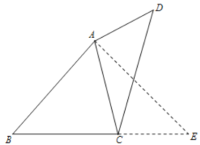
∵∠DAC+∠BCA=180°,

∠ECA+∠BCA=180°

∴∠DAC=∠ECA

在△ACD和△CAE中

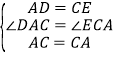
∴△ACD≌△CAE(SAS)

∴∠ACD=∠CAE,CD=AE,

∵∠BAC+∠ACD=90°

∴∠BAC+∠CAE=90°

∴∠BAE=90°

∵AB=CD,CD=AE

∴AB=AE

∴△BAE是等腰直角三角形

∴

∵,

∴

∵四边形 ABCD 的面积是 18

∴=18

∵CD>0,

∴CD=6

故答案为:6.