��Ŀ����
�Ķ����ϣ�
ѧϰ����������ij��ѧ��ȤС�鿪չ��һ��̽��������� �Ľ���ֵ��
�Ľ���ֵ��
С���ķ�����
��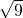 ��
�� ��
��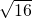 ��
��
�� =3+k��0��k��1����
=3+k��0��k��1����
��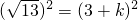 ��
��
��13=9+6k+k2��
��13��9+6k��
��� k�� ��
��
�� ��3+
��3+ ��3.67��
��3.67��
���⣺
��1����������С���ķ��������� �Ľ���ֵ��
�Ľ���ֵ��
��2��������������ʵ�������������� �Ĺ�ʽ����֪�Ǹ�����a��b��m����a��
�Ĺ�ʽ����֪�Ǹ�����a��b��m����a�� ��a+1����m=a2+b����
��a+1����m=a2+b���� ��______���ú�a��b�Ĵ���ʽ��ʾ����
��______���ú�a��b�Ĵ���ʽ��ʾ����
��3�����ã�2���еĽ��۹���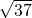 �Ľ���ֵ��
�Ľ���ֵ��
�⣺��1���� ��
�� ��
�� ��
��
�� =6+k��0��k��1����
=6+k��0��k��1����
�� ��
��
��41=36+12k+k2��
��41��36+12k��
���k�� ��
��
�� ��6+
��6+ ��6+0.42=6.42��
��6+0.42=6.42��
��2���� =a+k��0��k��1����
=a+k��0��k��1����
��m=a2+2ak+k2��a2+2ak��
��m=a2+b��
��a2+2ak=a2+b��
���k= ��
��
�� ��a+
��a+ ��
��
��3��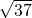 ��6+
��6+ ��6.08��
��6.08��
��������1��������Ŀ��Ϣ���ҳ�41ǰ�������ƽ�������Ӷ�ȷ���� =6+k��0��k��1�����ٸ�����Ŀ��Ϣ������⼴�ɣ�
=6+k��0��k��1�����ٸ�����Ŀ��Ϣ������⼴�ɣ�
��2��������Ŀ�ṩ���������kֵ��Ȼ���ټ���a���ɣ�
��3����a����6��b����1���빫ʽ���м��㼴�ɵý⣮
���������⿼�����������Ĺ��㣬������Ŀ�ṩ��Ϣ��Ȼ�������Ϣ�еķ����ı����ݼ��ɣ��ѶȲ�����Ȥζ�ԣ�
 ��
�� ��
�� ��
����
 =6+k��0��k��1����
=6+k��0��k��1������
 ��
����41=36+12k+k2��
��41��36+12k��
���k��
 ��
����
 ��6+
��6+ ��6+0.42=6.42��
��6+0.42=6.42����2����
 =a+k��0��k��1����
=a+k��0��k��1������m=a2+2ak+k2��a2+2ak��
��m=a2+b��
��a2+2ak=a2+b��
���k=
 ��
����
 ��a+
��a+ ��
����3��
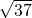 ��6+
��6+ ��6.08��
��6.08����������1��������Ŀ��Ϣ���ҳ�41ǰ�������ƽ�������Ӷ�ȷ����
 =6+k��0��k��1�����ٸ�����Ŀ��Ϣ������⼴�ɣ�
=6+k��0��k��1�����ٸ�����Ŀ��Ϣ������⼴�ɣ���2��������Ŀ�ṩ���������kֵ��Ȼ���ټ���a���ɣ�
��3����a����6��b����1���빫ʽ���м��㼴�ɵý⣮
���������⿼�����������Ĺ��㣬������Ŀ�ṩ��Ϣ��Ȼ�������Ϣ�еķ����ı����ݼ��ɣ��ѶȲ�����Ȥζ�ԣ�

��ϰ��ϵ�д�
�����Ŀ
 �Ķ����ϣ�������⣺
�Ķ����ϣ�������⣺





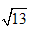 �Ľ���ֵ��
�Ľ���ֵ�� ��
��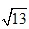 =3+k��0<k<1��.
=3+k��0<k<1��. ��2=��3+k��2
��2=��3+k��2 ��
��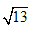 ��3+
��3+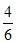 ��3.67��
��3.67��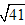 �Ľ���ֵ��
�Ľ���ֵ��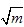 �Ĺ�ʽ����֪�Ǹ�����a��b��m����a<
�Ĺ�ʽ����֪�Ǹ�����a��b��m����a<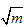 <a+1����m=a2+b����
<a+1����m=a2+b���� ��_________________(�ú�a��b�Ĵ���ʽ��ʾ)��
��_________________(�ú�a��b�Ĵ���ʽ��ʾ)�� �Ľ���ֵ.��
�Ľ���ֵ.��