题目内容
请阅读下面材料:已知点A、B在数轴上分别表示有理数a,b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a-b|;当A、B两点都不在原点时,①如图2,点A、B都在原点右边,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;②如图3,点A、B都在原点左边,|AB|=|OA|-|OB|=|a|-|b|=-a-(-b)=b-a=|a-b|;③如图4,点A、B在原点两边,|AB|=|OB|+|OA|=|b|+|a|=a+(-b)=|a-b|.
综上所述,数轴上A、B两点之间的距离表示为|AB|=|a-b|.
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是________,数轴上表示-2和-5的两点之间的距离是________,数轴上表示-2和5的两点之间的距离是__________;
(2)数轴上表示x和-1的两点A、B之间的距离是__________,如果|AB|=2,则x为_________;
(3)当代数式|x+1|+|x-2|取最小值时,相应的x有的取值范围是___________.
答案:
解析:
提示:
解析:
| (1)3,3,7;(2)|x+1|,1或-3;(3)-1≤x≤2.
|
提示:
| (3)代数式取得的最小值为0,而在数轴上可看出只要x在-1与2之间时代数式都为0
|

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
请阅读下面材料:
若 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.
为此抛物线的对称轴.
有一种方法证明如下:
证明:∵ ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点, ∴
(a ≠ 0)上不同的两点, ∴ 且
且  ≠
≠ .
.
①-②得 .
.
∴ .
.
∴ .
.
又∵ 抛物线 (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为 ,
,
∴ 直线 为此抛物线的对称轴.
为此抛物线的对称轴.
(1)反之,如果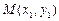 ,
,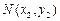 是抛物线
是抛物线 (a ≠ 0)上不同的两点,直线
(a ≠ 0)上不同的两点,直线 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取 ,
, 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
(2)利用以上结论解答下面问题:
已知二次函数 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
若
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.
为此抛物线的对称轴.有一种方法证明如下:
|
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点, ∴
(a ≠ 0)上不同的两点, ∴ 且
且  ≠
≠ .
. ①-②得
 .
.∴
 .
.∴
 .
.又∵ 抛物线
 (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为 ,
,∴ 直线
 为此抛物线的对称轴.
为此抛物线的对称轴.(1)反之,如果
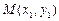 ,
,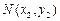 是抛物线
是抛物线 (a ≠ 0)上不同的两点,直线
(a ≠ 0)上不同的两点,直线 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取 ,
, 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;(2)利用以上结论解答下面问题:
已知二次函数
 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值. 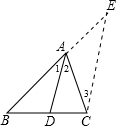 E∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
E∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明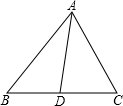 []
[] 为此抛物线的对称轴.
为此抛物线的对称轴. 且 x1≠x2.
且 x1≠x2.
 ,
, 为此抛物线的对称轴.
为此抛物线的对称轴. 为该抛物线的对称轴,那么自变量取x1,x2时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
为该抛物线的对称轴,那么自变量取x1,x2时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;