题目内容
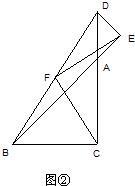
如图,点A在⊙O上,⊙O的直径为8,∠B=30°,∠C=90°,AC=8.将△ABC从AC与⊙O相切于点A的位置开始,绕着点A顺时针旋转,旋转角为β(0°<β<120°),旋转后AC,AB分别与⊙O交于点E,F,连接EF.当BC与⊙O相切时,①旋转角β= 度;②△AEF的面积为 .
【答案】分析:根据切线的性质,可以判断当BC与⊙O相切时切点一定是C旋转以后的对应点C′,AC′是圆的直径,即可求得旋转角,进而可以确定△AEF的位置,即可求解△AEF的面积.
解答: 解:设旋转以后BC与⊙O相切于点H,则连接OH,OA,则OH⊥BC,则OA=OH=4,AC=8,因而OA+OH=AC,
解:设旋转以后BC与⊙O相切于点H,则连接OH,OA,则OH⊥BC,则OA=OH=4,AC=8,因而OA+OH=AC,
则H一定与C重合.
故当BC与⊙O相切时切点一定是C旋转以后的对应点C′,AC′是圆的直径.
E就是点C′,
∵AC是切线,
∴∠CAA′=90°,即β=90°.
在直角△AC′F中,∠FAC′=60°,则AF= AC′=4,
AC′=4,
FC′= AC′=4
AC′=4 ,
,
则△AFC′的面积即△AEF的面积等于: AF•FC′=
AF•FC′= ×4×4
×4×4 =8
=8 .
.
故答案是:90,8 .
.
点评:本题考查了切线的性质,以及解直角三角形,正确判断当BC与圆相切时,切点的位置是关键.
解答:
 解:设旋转以后BC与⊙O相切于点H,则连接OH,OA,则OH⊥BC,则OA=OH=4,AC=8,因而OA+OH=AC,
解:设旋转以后BC与⊙O相切于点H,则连接OH,OA,则OH⊥BC,则OA=OH=4,AC=8,因而OA+OH=AC,则H一定与C重合.
故当BC与⊙O相切时切点一定是C旋转以后的对应点C′,AC′是圆的直径.
E就是点C′,
∵AC是切线,
∴∠CAA′=90°,即β=90°.
在直角△AC′F中,∠FAC′=60°,则AF=
 AC′=4,
AC′=4,FC′=
 AC′=4
AC′=4 ,
,则△AFC′的面积即△AEF的面积等于:
 AF•FC′=
AF•FC′= ×4×4
×4×4 =8
=8 .
.故答案是:90,8
 .
.点评:本题考查了切线的性质,以及解直角三角形,正确判断当BC与圆相切时,切点的位置是关键.

练习册系列答案
相关题目

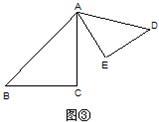
 27、附加题:
27、附加题: 如图,点D在AB上,DF交AC于点E,CF∥AB,AE=EC.
如图,点D在AB上,DF交AC于点E,CF∥AB,AE=EC.
 如图,点D在AB上,直线DG交AF于点E.请从①DG∥AC,②AF平分∠BAC,③AD=DE中任选两个作为条件,余下一个作为结论,构造一个真命题,并说明理由.已知:
如图,点D在AB上,直线DG交AF于点E.请从①DG∥AC,②AF平分∠BAC,③AD=DE中任选两个作为条件,余下一个作为结论,构造一个真命题,并说明理由.已知: