题目内容
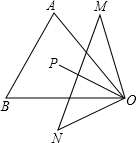已知∠AOB=45°，其内部有一点P关于OA的对称点是M，关于OB的对称点是N．且OP=4cm，则S△MON=________．
8cm2
分析：根据轴对称的性质可证∠MON=2∠AOB=90°；再利用OM=ON=OP，即可求出△MON的面积．
解答：根据题意得，OA垂直平分PM，OB垂直平分PN．
∴∠MOA=∠AOP，∠NOB=∠BOP；OM=OP=ON=4cm．
∴∠MON=2∠AOB=90°．
∴△MON的面积=
×4×4=8（cm2）．
故答案为：8cm2．
点评：此题考查了轴对称的性质及相关图形的面积计算，根据轴对称的性质得出∠MON=2∠AOB=90°是解题关键．
分析：根据轴对称的性质可证∠MON=2∠AOB=90°；再利用OM=ON=OP，即可求出△MON的面积．
解答：根据题意得，OA垂直平分PM，OB垂直平分PN．
∴∠MOA=∠AOP，∠NOB=∠BOP；OM=OP=ON=4cm．
∴∠MON=2∠AOB=90°．
∴△MON的面积=
×4×4=8（cm2）．故答案为：8cm2．
点评：此题考查了轴对称的性质及相关图形的面积计算，根据轴对称的性质得出∠MON=2∠AOB=90°是解题关键．
练习册系列答案
相关题目
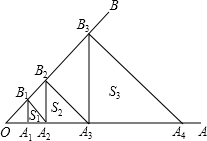如图，已知∠AOB=45°，A1是OA上的一点，且OA1=1，过A1作OA的垂线交OB于点B1，过点B1作OB的垂线交OA于点A2，过点A2作OA的垂线交OB于点B2…，依次记△A1B1A2，△A2B2A3，△A3B3A4…的面积为S1，S2，S3…，则Sn=
如图，已知∠AOB=45°，P为∠AOB内任一点，且OP=5，请在图中分别画出点P关于OA，OB的对称点P1，P2，连P1O，P2O，P1P2，则△OP1P2的面积为
已知∠AOB=45°，P是∠AOB内一点，且PO=4，M、N分别是OA、OB上的动点，则△PMN周长的最小值是
如图，已知∠AOB=45°，A1是OA上的一点，OA1=1，过A1作OA的垂线交OB于点B1，过点B1作OB的垂线交OA于点A2；过A2作OA的垂线交OB于点B2…如此继续，依次记△A1B1A2，△A2B2A3，△A3B3A4…的面积为S1，S2，S3…，则S2011=