题目内容
已知⊙O的半径为26cm，弦AB∥CD，AB=48cm，CD=20cm，则AB、CD之间的距离为 ．
【答案】分析：首先作AB、CD的垂线EF，然后根据垂径定理求得CE=DE=10cm，AF=BF=24cm；再在直角三角形OED和直角三角形OBF中，利用勾股定理求得OE、OF的长度；最后根据图示的两种情况计算EF的长度即可．
解答：解：有两种情况．如图．过O作AB、CD的垂线EF，交AB于点F，交CD于点E．
∴EF就是AB、CD间的距离．
∵AB=48cm，CD=20cm，根据垂径定理，得 CE=DE=10cm，AF=BF=24cm，
∵OD=OB=26cm，
∴在直角三角形OED和直角三角形OBF中，
∴OE=24cm，OF=10cm（勾股定理），
∴①EF=24+10=34cm ②EF=24-10=14cm．
故答案为：34或14cm．
点评：本题考查了勾股定理、垂径定理的综合运用．解答此题时，要分类讨论，以防漏解．
解答：解：有两种情况．如图．过O作AB、CD的垂线EF，交AB于点F，交CD于点E．
∴EF就是AB、CD间的距离．
∵AB=48cm，CD=20cm，根据垂径定理，得 CE=DE=10cm，AF=BF=24cm，
∵OD=OB=26cm，
∴在直角三角形OED和直角三角形OBF中，
∴OE=24cm，OF=10cm（勾股定理），
∴①EF=24+10=34cm ②EF=24-10=14cm．
故答案为：34或14cm．
点评：本题考查了勾股定理、垂径定理的综合运用．解答此题时，要分类讨论，以防漏解．
练习册系列答案
相关题目
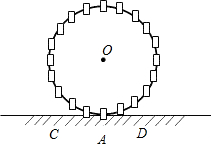游乐园的大观览车半径为26米，如图所示，已知观览车绕圆心O顺时针作匀速运动，旋转一周用12分钟．小丽从观览车的最低处（底面A处）乘车，问经过4分钟后，
点P在直线l上运动．