题目内容
 已知⊙O是△ABC的外接圆,⊙O半径为R,AD是△ABC的高,E是
已知⊙O是△ABC的外接圆,⊙O半径为R,AD是△ABC的高,E是 的中点,EF与⊙O切于E,交AC的延长线于F,则下列结论:
的中点,EF与⊙O切于E,交AC的延长线于F,则下列结论:
①AC•AB=2R•AD; ②EF∥BC; ③CF•AC=EF•CM; ④ .
.
其中正确的结论是
- A.①②③
- B.①③④
- C.②③④
- D.①②③④
D
分析:①连接AO并延长交⊙O于G点,连接CG,则∠GCA=∠ADB=90°,∠G=∠B,证明△ACG∽△ADB,利用相似比证明结论;
②连接OE,由EF为⊙O的切线可知OE⊥EF,由E是 的中点可知OE⊥BC,故结论成立;
的中点可知OE⊥BC,故结论成立;
③连接CE,证明△ACM∽△EFC,利用相似比证明结论;
④过M点分别作MP⊥AC,MQ⊥AB,由E是 的中点可知AE平分∠BAC,由角平分线的性质得MP=MQ,而∠F=∠PCM,在Rt△PCM和Rt△BDQ中,分别表示sin∠B,sin∠PCM,再求比.
的中点可知AE平分∠BAC,由角平分线的性质得MP=MQ,而∠F=∠PCM,在Rt△PCM和Rt△BDQ中,分别表示sin∠B,sin∠PCM,再求比.
解答: 解:①如图1,连接AO并延长交⊙O于G点,连接CG,
解:①如图1,连接AO并延长交⊙O于G点,连接CG,
∵AG为直径,∴∠GCA=∠ADB=90°,又∠G=∠B,
∴△ACG∽△ADB,∴ =
= ,AG=2R,∴AC•AB=2R•AD,①正确;
,AG=2R,∴AC•AB=2R•AD,①正确;
②如图1,连接OE,
∵EF为⊙O的切线,E为切点,∴OE⊥EF,
又∵E是 的中点,∴OE⊥BC,
的中点,∴OE⊥BC,
∴EF∥BC,②正确;
③如图2,连接CE,
∵EF∥BC,∴∠ACM=∠F,
由弦切角定理可知∠CAE=∠FEC,∴△ACM∽△EFC,
∴ =
= ,即CF•AC=EF•CM,③正确;
,即CF•AC=EF•CM,③正确;
④如图2,过M点分别作MP⊥AC,MQ⊥AB,垂足为P,Q,
∵E是 的中点,∴AE平分∠BAC,∴MP=MQ,
的中点,∴AE平分∠BAC,∴MP=MQ,
又∠F=∠PCM,∴在Rt△PCM中,sin∠PCM=sinF= ,
,
在Rt△BDQ中,sinB= ,
,
∴ =
=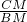 ,④正确.
,④正确.
故选D.
点评:本题考查了切线的性质,平行线的判定与性质,圆周角定理,相似三角形的判定与性质,角平分线的判定与性质,锐角三角函数的定义.关键是通过作辅助线,将问题转化到直角三角形中求解.
分析:①连接AO并延长交⊙O于G点,连接CG,则∠GCA=∠ADB=90°,∠G=∠B,证明△ACG∽△ADB,利用相似比证明结论;
②连接OE,由EF为⊙O的切线可知OE⊥EF,由E是
 的中点可知OE⊥BC,故结论成立;
的中点可知OE⊥BC,故结论成立;③连接CE,证明△ACM∽△EFC,利用相似比证明结论;
④过M点分别作MP⊥AC,MQ⊥AB,由E是
 的中点可知AE平分∠BAC,由角平分线的性质得MP=MQ,而∠F=∠PCM,在Rt△PCM和Rt△BDQ中,分别表示sin∠B,sin∠PCM,再求比.
的中点可知AE平分∠BAC,由角平分线的性质得MP=MQ,而∠F=∠PCM,在Rt△PCM和Rt△BDQ中,分别表示sin∠B,sin∠PCM,再求比.解答:
 解:①如图1,连接AO并延长交⊙O于G点,连接CG,
解:①如图1,连接AO并延长交⊙O于G点,连接CG,∵AG为直径,∴∠GCA=∠ADB=90°,又∠G=∠B,
∴△ACG∽△ADB,∴
 =
= ,AG=2R,∴AC•AB=2R•AD,①正确;
,AG=2R,∴AC•AB=2R•AD,①正确;②如图1,连接OE,
∵EF为⊙O的切线,E为切点,∴OE⊥EF,
又∵E是
 的中点,∴OE⊥BC,
的中点,∴OE⊥BC,∴EF∥BC,②正确;
③如图2,连接CE,
∵EF∥BC,∴∠ACM=∠F,

由弦切角定理可知∠CAE=∠FEC,∴△ACM∽△EFC,
∴
 =
= ,即CF•AC=EF•CM,③正确;
,即CF•AC=EF•CM,③正确;④如图2,过M点分别作MP⊥AC,MQ⊥AB,垂足为P,Q,
∵E是
 的中点,∴AE平分∠BAC,∴MP=MQ,
的中点,∴AE平分∠BAC,∴MP=MQ,又∠F=∠PCM,∴在Rt△PCM中,sin∠PCM=sinF=
 ,
,在Rt△BDQ中,sinB=
 ,
,∴
 =
=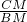 ,④正确.
,④正确.故选D.
点评:本题考查了切线的性质,平行线的判定与性质,圆周角定理,相似三角形的判定与性质,角平分线的判定与性质,锐角三角函数的定义.关键是通过作辅助线,将问题转化到直角三角形中求解.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
已知α,β是△ABC的两个角,且sinα,tanβ是方程2x2-3x+1=0的两根,则△ABC是( )
| A、锐角三角形 | B、直角三角形或钝角三角形 | C、钝角三角形 | D、等边三角形 |
已知O是△ABC的外心,∠ABC=60°,AC=4,则△ABC外接圆的半径是( )
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
 9、如图,已知AD是△ABC的角平分线,CE⊥AD,垂足O,CE交AB于E,则下列命题:①AE=AC,②CO=OE,③∠AEO=∠ACO,④∠B=∠ECB.其中正确的是( )
9、如图,已知AD是△ABC的角平分线,CE⊥AD,垂足O,CE交AB于E,则下列命题:①AE=AC,②CO=OE,③∠AEO=∠ACO,④∠B=∠ECB.其中正确的是( ) F⊥AB于F,且CE=CF.
F⊥AB于F,且CE=CF. 如图,已知BE是△ABC的高,AE=BE,
如图,已知BE是△ABC的高,AE=BE,