题目内容
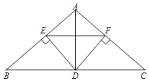
【题目】已知，如图，线段
长为
，
于
，
于
，
＝
，
＝
，
为线段上两动点，
在
右侧且＝
，则由
到
的路径：
的最小值为________．
【答案】
【解析】
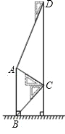
过
作
且
＝
＝
，作
关于
的对称点″，连接″
交于点
，过作
交于
，由AA′//EF，AE//A′F可得四边形AEFA′是平行四边形，根据平行四边形的性质可得AE=A′F，根据轴对称的性质可得A′F=A″F，即可得出
的最小值＝″，进而可得
的值最小，过″作″
交
的延长线于
，利用勾股定理求出″的值即可求出的值.
过作且＝＝，作关于的对称点″，连接″交于点，过作交于，
∵AA′//EF，AE//A′F，
∴四边形AEFA′是平行四边形，
∴AE=A′F，
∵A′和A″关于CD对称，
∴A′F=A″F，
∴AE+FB=A″F+FB
∴的最小值＝″，此时，的值最小，的最小值＝″，
过″作″交的延长线于，
则″＝
，
＝
，
∴″＝
=
，
∴的最小值为，
练习册系列答案
相关题目
