题目内容
(2009•德化县质检)已知直线l1: 与直线l2:
与直线l2: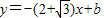 相交于点B(
相交于点B(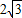 ,2),且直线l2与x轴相交于点A.
,2),且直线l2与x轴相交于点A.(1)求A点的坐标;
(2)点C在线段AB上,过C点作CD∥OB,交x轴于D点,已知以线段CD为直径的⊙M与直线l1相切.
①求⊙M的半径r;
②若把△OAB绕着原点O逆时针旋转90°得到△OA'B',在y轴上是否存在一点P,使得⊙P与⊙M、以OA'为直径的⊙N都相切?若存在,请求出P点的坐标;若不存在,请说明理由.
【答案】分析:本题先由两直线相交于点B,求出b值,进而求出点A的坐标.(2)问中要根据题意画出图形,按照直线与圆的几种位置关系列出关系式求解.
解答: 解:(1)依题意可知:
解:(1)依题意可知:
y=-2(2+ )×2
)×2 +b,
+b,
解得:b=8+4 ;
;
∴直线l2:y=-(2+ )x+8+4
)x+8+4 .
.
由y=0得:0=-(2+ )x+8+4
)x+8+4 ,解得x=4;
,解得x=4;
∴A(4,0).
(2)①设点M到直线l1的距离为d,过点A作AE⊥l1于点E;
在Rt△AOE中,AE= ,OA=2,
,OA=2,
∵CD∥l1,
∴ ,
,
∴d=2-r;
∵OM与l1相切,
∴2-r=r,即r=1;
②容易求得M(2+ ,
, ),
),
设⊙P的半径为R,
根据两圆相切的性质可得:
(一)当⊙P与⊙M、⊙N都外切时,得:
(R+1)2=(2+ )2+(R+
)2+(R+ )2,解得R=4+
)2,解得R=4+ ,
,
∴P1(0,-4- ),
),
(二)当⊙N、⊙M都与⊙P内切时,得:
(R-1)2=(2+ )2+(R-
)2+(R- )2,
)2,
解得R=
∴P2(0, );
);
综上所述,满足条件的P点的坐标为P1(0,-4- ),P2(0,
),P2(0, ).
).
点评:本题综合考查了一次函数与几何知识的应用,题中运用圆与直线的关系以及直角三角形等知识求出线段的长是解题的关键.
解答:
 解:(1)依题意可知:
解:(1)依题意可知:y=-2(2+
 )×2
)×2 +b,
+b,解得:b=8+4
 ;
;∴直线l2:y=-(2+
 )x+8+4
)x+8+4 .
.由y=0得:0=-(2+
 )x+8+4
)x+8+4 ,解得x=4;
,解得x=4;∴A(4,0).
(2)①设点M到直线l1的距离为d,过点A作AE⊥l1于点E;
在Rt△AOE中,AE=
 ,OA=2,
,OA=2,∵CD∥l1,
∴
 ,
,∴d=2-r;
∵OM与l1相切,
∴2-r=r,即r=1;
②容易求得M(2+
 ,
, ),
),设⊙P的半径为R,
根据两圆相切的性质可得:
(一)当⊙P与⊙M、⊙N都外切时,得:
(R+1)2=(2+
 )2+(R+
)2+(R+ )2,解得R=4+
)2,解得R=4+ ,
,
∴P1(0,-4-
 ),
),(二)当⊙N、⊙M都与⊙P内切时,得:
(R-1)2=(2+
 )2+(R-
)2+(R- )2,
)2,解得R=

∴P2(0,
 );
);综上所述,满足条件的P点的坐标为P1(0,-4-
 ),P2(0,
),P2(0, ).
).点评:本题综合考查了一次函数与几何知识的应用,题中运用圆与直线的关系以及直角三角形等知识求出线段的长是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(2009•德化县质检)某陶瓷公司招工广告称:“本公司工人工作时间:每天工作8小时,每月工作25天;待遇:工人按计件付工资,每月另加生活费100元,按月结算…”.该公司只生产甲、乙两种陶瓷,工人小王记录了如下一些数据:
(1)设生产每个甲种陶瓷所需的时间为m分钟,用含有m的代数式表示生产每个乙种陶瓷所需的时间;
(2)设小王工人小王某月(工作25天)生产甲种陶瓷x个,乙种陶瓷y个,
①试求y与x的函数关系式;(不需写出自变量x的取值范围)
②根据市场调查,每个工人每月生产甲种陶瓷的数量不少于乙种陶瓷数量的 倍,且生产每个乙种陶瓷的计件工资可提高0.2元,甲种陶瓷计件工资也有提高的空间.若小王的工作效率不变,甲种陶瓷计件工资至少要提高多少元,小王的月工资(计件工资+福利工资=月工资)才能领到1200元?
倍,且生产每个乙种陶瓷的计件工资可提高0.2元,甲种陶瓷计件工资也有提高的空间.若小王的工作效率不变,甲种陶瓷计件工资至少要提高多少元,小王的月工资(计件工资+福利工资=月工资)才能领到1200元?
| 甲种陶瓷 (单位:个) | 乙种陶瓷 (单位:个) | 总时间 (单位:分钟) | 计件工资 (单位:元) |
| 1 | 1 | 35 | 2.8 |
| 3 | 2 | 85 | 6.6 |
(2)设小王工人小王某月(工作25天)生产甲种陶瓷x个,乙种陶瓷y个,
①试求y与x的函数关系式;(不需写出自变量x的取值范围)
②根据市场调查,每个工人每月生产甲种陶瓷的数量不少于乙种陶瓷数量的
 倍,且生产每个乙种陶瓷的计件工资可提高0.2元,甲种陶瓷计件工资也有提高的空间.若小王的工作效率不变,甲种陶瓷计件工资至少要提高多少元,小王的月工资(计件工资+福利工资=月工资)才能领到1200元?
倍,且生产每个乙种陶瓷的计件工资可提高0.2元,甲种陶瓷计件工资也有提高的空间.若小王的工作效率不变,甲种陶瓷计件工资至少要提高多少元,小王的月工资(计件工资+福利工资=月工资)才能领到1200元?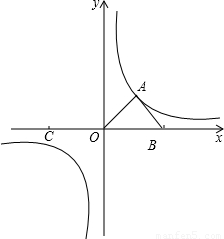
 .
.