题目内容
在△ABC中，∠B=2∠C，下列结论成立的是（ ）
| A．AC=2AB |
| B．AC＜2AB |
| C．AC＞2AB |
| D．AC与2AB大小关系不确定 |
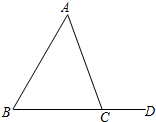
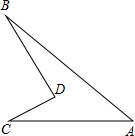
如图，延长CB至D，使BD=AB，连接AD，
∵BD=AB，
∴∠D=∠DAB，
又∵∠ABC=∠D+∠DAB=2∠D，∠B=2∠C，
∴∠D=∠C，
∴AD=AC．
再根据三角形的两边之和大于第三边，
得：AD＜BD+AB=2AB，即AC＜2AB．
故选B．
∵BD=AB，
∴∠D=∠DAB，
又∵∠ABC=∠D+∠DAB=2∠D，∠B=2∠C，
∴∠D=∠C，
∴AD=AC．
再根据三角形的两边之和大于第三边，
得：AD＜BD+AB=2AB，即AC＜2AB．
故选B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
