题目内容
 如图,在⊙O中,直径AB的长为
如图,在⊙O中,直径AB的长为 ,弦CD⊥AB于E,∠BDC=30°则弦CD的长为________.
,弦CD⊥AB于E,∠BDC=30°则弦CD的长为________.
3
分析:连接BD,由∠BDC=30°,即可推出∠BOC=60°,再由AB的长为 ,求出OC的长度,然后根据特殊角的三角函数值即可推出CE的长度,最后由垂径定理推出CD=2CE,通过计算即可求出CD的长度.
,求出OC的长度,然后根据特殊角的三角函数值即可推出CE的长度,最后由垂径定理推出CD=2CE,通过计算即可求出CD的长度.
解答:连接BD,
∵∠BDC=30°,
∴∠BOC=60°,
∵AB= ,
,
∴OC= ,
,
∵CD⊥AB,
∴∠OEC=90°,CD=2CE,
∴cos30°=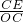 =
= ,
,
∵OC= ,
,
∴CE= ,
,
∴CD=3.
故答案为3.

点评:本题主要考查圆周角定理,特殊角的三角函数值,垂径定理等知识点,关键在于首先运用圆周角定理推出∠COE的度数,然后根据特殊角的三角函数值推出CE的长度,最后根据垂径定理即可推出CD的长度.
分析:连接BD,由∠BDC=30°,即可推出∠BOC=60°,再由AB的长为
 ,求出OC的长度,然后根据特殊角的三角函数值即可推出CE的长度,最后由垂径定理推出CD=2CE,通过计算即可求出CD的长度.
,求出OC的长度,然后根据特殊角的三角函数值即可推出CE的长度,最后由垂径定理推出CD=2CE,通过计算即可求出CD的长度.解答:连接BD,
∵∠BDC=30°,
∴∠BOC=60°,
∵AB=
 ,
,∴OC=
 ,
,∵CD⊥AB,
∴∠OEC=90°,CD=2CE,
∴cos30°=
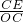 =
= ,
,∵OC=
 ,
,∴CE=
 ,
,∴CD=3.
故答案为3.

点评:本题主要考查圆周角定理,特殊角的三角函数值,垂径定理等知识点,关键在于首先运用圆周角定理推出∠COE的度数,然后根据特殊角的三角函数值推出CE的长度,最后根据垂径定理即可推出CD的长度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
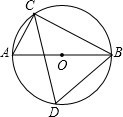 如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=
如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=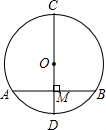 如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.
如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长. C与直线AB相交于点G.
C与直线AB相交于点G. (2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( )
(2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( ) (2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )
(2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )