题目内容
若关于x的方程3(x-1)(x-2m)=(m-12)x的两根之和与两根之积相等,则方程的根为
9±3
| 7 |
9±3
.| 7 |
分析:先将方程整理成一般形式:3x2+(9-7m)x+6m=0,再根据一元二次方程根与系数的关系列出关于m的方程-
=2m,解方程求出m=9,然后将m=9代入原方程,整理得到x2-18x+18=0,用求根公式求解即可.
| 9-7m |
| 3 |
解答:解:∵3(x-1)(x-2m)=(m-12)x,
∴3x2+(9-7m)x+6m=0,
由题意,得-
=2m,
解得m=9.
把m=9代入原方程,整理得x2-18x+18=0,
解得x=9±3
.
故答案为9±3
.
∴3x2+(9-7m)x+6m=0,
由题意,得-
| 9-7m |
| 3 |
解得m=9.
把m=9代入原方程,整理得x2-18x+18=0,
解得x=9±3
| 7 |
故答案为9±3
| 7 |
点评:本题考查了一元二次方程根与系数的关系及求根公式,解题的关键是注意掌握一元二次方程的两根x1、x2之间的关系:x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
若关于x的方程(x-2)+3k=
的根是负数,则k的取值范围是( )
| x+k |
| 3 |
A、k>
| ||
B、k≥
| ||
C、k<
| ||
D、k≤
|
若关于x的方程(m-1)xm2+1+5x+2=0是一元二次方程,则m的值等于( )
| A、1 | B、-1 | C、±1 | D、0 |
若关于x的方程3x+a=0的解比方程-
x-4=0的解大2,则a的值( )
| 2 |
| 3 |
| A、-18 | B、12 |
| C、24 | D、-12 |
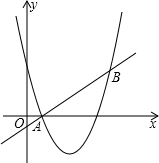 直线y=x+a和抛物线y=x2+bx+c都经过A(1,0)、B(3,2)两点,且不等式x+a>x2+bx+c 的整数解为K,若关于x的方程x2-(m2+5)x+2m2+6=0的两实根之差的绝对值为n,且n满足n=2(K+1),求m的值.
直线y=x+a和抛物线y=x2+bx+c都经过A(1,0)、B(3,2)两点,且不等式x+a>x2+bx+c 的整数解为K,若关于x的方程x2-(m2+5)x+2m2+6=0的两实根之差的绝对值为n,且n满足n=2(K+1),求m的值.