题目内容
如图,已知∠ABC=90°,AB=BC.直线l与以BC为直径的圆O相切于点C.点F是圆O上异于B、C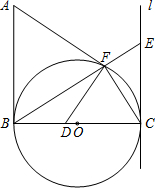 的动点,直线BF与l相交于点E,过点F作AF的垂线交直线BC与点D.
的动点,直线BF与l相交于点E,过点F作AF的垂线交直线BC与点D.(1)如果BE=15,CE=9,求EF的长;
(2)证明:①△CDF∽△BAF;②CD=CE;
(3)探求动点F在什么位置时,相应的点D位于线段BC的延长线上,且使BC=
| 3 |
分析:(1)由直线l与以BC为直径的圆O相切于点C,即可得∠BCE=90°,∠BFC=∠CFE=90°,则可证得△CEF∽△BEC,然后根据相似三角形的对应边成比例,即可求得EF的长;
(2)①由∠FCD+∠FBC=90°,∠ABF+∠FBC=90°,根据同角的余角相等,即可得∠ABF=∠FCD,同理可得∠AFB=∠CFD,则可证得△CDF∽△BAF;
②由△CDF∽△BAF与△CEF∽△BCF,根据相似三角形的对应边成比例,易证得
=
,又由AB=BC,即可证得CD=CE;
(3)由CE=CD,可得BC=
CD=
CE,然后在Rt△BCE中,求得tan∠CBE的值,即可求得∠CBE的度数,则可得F在⊙O的下半圆上,且
=
.
(2)①由∠FCD+∠FBC=90°,∠ABF+∠FBC=90°,根据同角的余角相等,即可得∠ABF=∠FCD,同理可得∠AFB=∠CFD,则可证得△CDF∽△BAF;
②由△CDF∽△BAF与△CEF∽△BCF,根据相似三角形的对应边成比例,易证得
| CD |
| BA |
| CE |
| BC |
(3)由CE=CD,可得BC=
| 3 |
| 3 |
 |
| BF |
| 2 |
| 3 |
 |
| BC |
解答:(1)解:∵直线l与以BC为直径的圆O相切于点C.
∴∠BCE=90°,
又∵BC为直径,
∴∠BFC=∠CFE=90°,
∵∠FEC=∠CEB,
∴△CEF∽△BEC,
∴
=
,
∵BE=15,CE=9,
即:
=
,
解得:EF=
;
(2)证明:①∵∠FCD+∠FBC=90°,∠ABF+∠FBC=90°,
∴∠ABF=∠FCD,
同理:∠AFB=∠CFD,
∴△CDF∽△BAF;
②∵△CDF∽△BAF,
∴
=
,
又∵∠FCE=∠CBF,∠BFC=∠CFE=90°,
∴△CEF∽△BCF,
∴
=
,
∴
=
,
又∵AB=BC,
∴CE=CD;

(3)解:∵CE=CD,
∴BC=
CD=
CE,
在Rt△BCE中,tan∠CBE=
=
,
∴∠CBE=30°,
故
为60°,
∴F在直径BC下方的圆弧上,且
=
.
∴∠BCE=90°,
又∵BC为直径,
∴∠BFC=∠CFE=90°,
∵∠FEC=∠CEB,
∴△CEF∽△BEC,
∴
| CE |
| BE |
| EF |
| CE |

∵BE=15,CE=9,
即:
| 9 |
| 15 |
| EF |
| 9 |
解得:EF=
| 27 |
| 5 |
(2)证明:①∵∠FCD+∠FBC=90°,∠ABF+∠FBC=90°,
∴∠ABF=∠FCD,
同理:∠AFB=∠CFD,
∴△CDF∽△BAF;
②∵△CDF∽△BAF,
∴
| CF |
| BF |
| CD |
| BA |
又∵∠FCE=∠CBF,∠BFC=∠CFE=90°,
∴△CEF∽△BCF,
∴
| CF |
| BF |
| CE |
| BC |
∴
| CD |
| BA |
| CE |
| BC |
又∵AB=BC,
∴CE=CD;

(3)解:∵CE=CD,
∴BC=
| 3 |
| 3 |
在Rt△BCE中,tan∠CBE=
| CE |
| BC |
| 1 | ||
|
∴∠CBE=30°,
故
 |
| CF |
∴F在直径BC下方的圆弧上,且
 |
| BF |
| 2 |
| 3 |
 |
| BC |
点评:此题考查了相似三角形的判定与性质,圆的切线的性质,圆周角的性质以及三角函数的性质等知识.此题综合性很强,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 24、如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH.
24、如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH. 如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.
如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°. 17、(1)已知线段a,h,用直尺和圆规作等腰三角形ABC,底边BC=a,BC边上的高为h(要求尺规作图,不写作法和证明)
17、(1)已知线段a,h,用直尺和圆规作等腰三角形ABC,底边BC=a,BC边上的高为h(要求尺规作图,不写作法和证明)
 20、如图,已知△ABC是锐角三角形,且∠A=50°,高BE、CF相交于点O,求∠BOC的度数.
20、如图,已知△ABC是锐角三角形,且∠A=50°,高BE、CF相交于点O,求∠BOC的度数.