题目内容

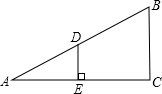
如图，已知△ADE和△ABC是位似图形，∠A=30°，DE垂直平分AC，且DE=2．
（1）求∠C的度数；
（2）求BC的长度．
（1）∵DE垂直平分AC，
∴∠AED=90°，
∵△ADE和△ABC是位似图形，
∴△ABC∽△ADE，
∴∠C=∠AED=90°；

（2）证明：∵△ABC∽△ADE，
∴
DE
BC
=
AE
AC
=
1
2
，
∴BC=2DE=2×2=4．
或用锐角三角函数求（简解如下）
由AE=
DE
tan30°
=2
3
，得到AC=4
3
，
∴BC=AC•tan30°=4
3
×
3
3
=4．
练习册系列答案
相关题目
阅读：如图①，以原点O为位似中心按比例尺（OA′：OA）3：1在位似中心的同侧将△OAB放大为△OA′B′，观察得到各点的坐标见表一，可以归纳得出：对应点的横、纵坐标均存在3倍的关系，即P（x，y）的对应点P′的坐标为（3x，3y）．仿照图①，按要求完成下列画图并将坐标与归纳猜想填入表格相应．

活动一：在图②中，以点T（1，1）为位似中心按比例尺（TE′：TE）3：1在位似中心的同侧将△TEF放大为△TE′F′，并将点E′、F′的坐标和归纳猜想填入表二；
活动二：在图③中，以点W（2，3）为位似中心按比例尺（WG′：WG）4：1在位似中心的同侧将△WGH放大为△WG′H′，并将点G′、H′的坐标和归纳猜想填入表三；
表格表一表二表三
位似中心O（0，0）T（1，1）W（2，3）
比例尺3：13：14：1
点的坐标A（1，2）B（3，1）E（2，3）F（4，2）G（3，5）H（5，4）
对应点坐标A′（3，6）B（9，3）E′（　　）F′（　　）G′（　　）H′（　　）
猜想结论点P（x，y）的对应点P′的坐标为（3x，3y）点P（x，y）的对应点P′的坐标为（　　）点Q（x，y）的对应点Q′的坐标为（　　）
活动三：归纳结论：以点M（a，b）为位似中心，按比例尺（MP′：MP）n：1在位似中心的同侧将图形放大，则点R（x，y）的对应点R′的横坐标为______，纵坐标为______．
（1）如图1，△ABC中，AB=AC=BC，P为AC上一点，过P点可作______条直线将△ABC分成两部分，使截得的三角形与△ABC相似；作出直线草图．
（2）如图2，△ABC中，∠C=90°，P为斜边AB上的一点，过P点可作______条直线将△ABC分成两部分，使截得的三角形与△ABC相似；作出直线草图．
（3）如图3，△ABC中AB＞AC，P点为AC上一点，过P点可作______条直线将△ABC分成两部分，使截得的三角形与△ABC相似，作出直线草图．
如图所示，在14×18的网格中建立平面直角坐标系，△ABC的顶点在格点上，点A的坐标为（1，1）．
（1）把△ABC绕点A按逆时针方向旋转90°后得到△AB1C1，请画出△AB1C1的图形，并写出C1的坐标；
（2）把△ABC以点O为位似中心放大，使放大前后对应边的比为1﹕2，在第一象限内画出放大后的△A2B2C2的图形．
如图，矩形ABCD的坐标分别为A（-2，1），B（-2，4），C（-6，4），D（6，1），画出它的一个以原点O为位似中心，相似比为
1
2
的位似图形．
如图所示，在正方形网格上有一个三角形ABC，请在该正方形网格中尽可能多地画出与它相似的三角形（要求：顶点在格点上，与原三角形不全等）．
已知△ABC的三个顶点坐标如下表：
（1）将下表补充完整，并在直角坐标系中，画出△A′B′C′；

（2）观察△ABC与△A′B′C′，写出有关这两个三角形关系的一个正确结论．
如图，在对Rt△OAB依次进行位似、轴对称和平移变换后得到△O′A′B′．
（1）在坐标纸上画出这几次变换相应的图形；
（2）设P（x，y）为△OAB边上任一点，依次写出这几次变换后点P对应点的坐标．
如图所示的网格中，每个小方格都是边长为1的小正方形，B点的坐标为：B（-1，-1）．
（1）把△ABC绕点C按顺时针旋转90°后得到△A1B1C1，请画出这个三角形并写出点B1的坐标；
（2）以点A为位似中心放大△ABC，得到△A2B2C2，使放大前后的面积之比为1：4请在下面网格内画出△A2B2C2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网