题目内容
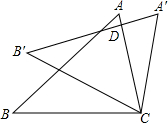如图，把△ABC绕点C顺时针旋转25°，得到△A′B′C，A′B′交AC于点D，若∠A′DC=90°，则∠A=________．
65°
分析：根据旋转的性质对应点与旋转中心的连线段的夹角等于旋转角得到∠ACA′=25°，而∠A′DC=90°，则∠A′=90°-25°=65°，然后再根据旋转的性质即可得到∠A=65°．
解答：∵△ABC绕点C顺时针旋转25°，得到△A′B′C，
∴∠ACA′=25°，
又∵∠A′DC=90°，
∴∠A′=90°-25°=65°，
∴∠A=65°．
故答案为65°．
点评：本题考查了旋转的性质：旋转前后两图形全等，即对应角相等，对应边相等，对应点与旋转中心的连线段的夹角等于旋转角．
分析：根据旋转的性质对应点与旋转中心的连线段的夹角等于旋转角得到∠ACA′=25°，而∠A′DC=90°，则∠A′=90°-25°=65°，然后再根据旋转的性质即可得到∠A=65°．
解答：∵△ABC绕点C顺时针旋转25°，得到△A′B′C，
∴∠ACA′=25°，
又∵∠A′DC=90°，
∴∠A′=90°-25°=65°，
∴∠A=65°．
故答案为65°．
点评：本题考查了旋转的性质：旋转前后两图形全等，即对应角相等，对应边相等，对应点与旋转中心的连线段的夹角等于旋转角．
练习册系列答案
全能测控一本好卷系列答案
相关题目
9、如图，把△ABC绕点C顺时针旋转35°后，得到△A′B′C，A′B′交AC于点D，若∠A′DC=90°，则∠A的度数是（ ）
14、如图，把△ABC绕点C顺时针旋转22度，得△A1B1C，则直线AB与A1B1所成的锐角为
18、如图，把△ABC绕点A顺时针旋转120°得到△ADE，如果∠CAD=50°，则∠DAE=
如图，把△ABC绕点C顺时针旋转43°，得到△A′B′C，A′B′交AC于点D，若∠A′DC=90°，则∠A=
如图，把△ABC绕点A按顺时针方向旋转90°到△AB′C′．