题目内容
如图，平行四边形ABCD中，E为AD延长线上的一点，D为AE的一个黄金分割点，即AD=
AE，BE交DC于点F．若CF=2，则AB的长为________．
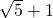
分析：先由AD=
AE，得出DE=
AE，再根据平行四边形的性质得出DF∥AB，DC=AB，从而得出△EDF∽△EAB，根据相似三角形比例关系即可得出答案．解答：∵AD=
AE，∴DE=
AE．∵四边形ABCD为平行四边形，
∴DF∥AB，DC=AB，
∴△EDF∽△EAB，
∴
=
，∴
=，解得AB=
+1．故答案为：
+1．点评：本题主要考查了平行四边形的性质，相似三角形的判定和性质，难度适中．
练习册系列答案
相关题目
次方程x2-7x+12=0的两个根，且OA＞OB．
10、如图，平行四边形ABCD中，∠ABC的角平分线BE交AD于E点，AB=3，ED=1，则平行四边形ABCD的周长是
如图，平行四边形ABCD中，对角线AC和BD相交于点O，如果AC=12，BD=10，AB=m，那么m的取值范围是
如图，平行四边形ABCD的两条对角线AC、BD相交于点O，AB=5，AC=6，DB=8，则四边形ABCD是的周长为