题目内容

试判断如下以a、b、c为边长的三角形，其中不是直角三角形的是

A.
c的关系满足a²-b²=c²
B.
a=1，b=2， $数学公式$
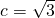
C.
a=m²+n²，b=mn，c=m²-n²（m＞n＞0）
D.
a：b：c=5：12：13

C
分析：利用勾股定理的逆定理进行判断即可．
解答：A、由于a²-b²=c²，易得a²=b²+c²，从而可知此三角形是直角三角形，故此选项错误；
B、由于1²+（ $\text{[math]}$ ）²=2²=4，从而可知此三角形是直角三角形，故此选项错误；
C、由于b²+c²=m⁴-m²n²+n⁴≠a²，从而可知此三角形不是直角三角形，故此选项正确；
D、可设a=5x，b=12x，c=13x，那么易得a2+b2=c2，从而可知此三角形是直角三角形，故此选项错误．
故选C．
点评：本题考查了勾股定理的逆定理．解题的关键是灵活运用勾股定理的逆定理．

练习册系列答案

课堂在线系列答案

同步大冲关系列答案

状元桥优质课堂系列答案

启东培优微专题系列答案

初中单元练习与测试系列答案

优质课堂快乐成长系列答案

智慧大考卷系列答案

导学案广东经济出版社系列答案

优佳好书系讲与练系列答案

课课练与单元检测系列答案

相关题目

试判断如下以a、b、c为边长的三角形，其中不是直角三角形的是（　　）

A、c的关系满足a²-b²=c²

B、a=1，b=2，c=

C、a=m²+n²，b=mn，c=m²-n²（m＞n＞0）

D、a：b：c=5：12：13

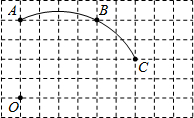如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．
（1）请完成如下操作：
①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长，建立平面直角坐标系；②用直尺和圆规画出该圆弧所在圆的圆心D的位置（不用写作法，保留作图痕迹），并连接AD、CD．
（2）请在（1）的基础上，完成下列问题：
①写出点的坐标：C

；
②⊙D的半径=

（结果保留根号）；
③若扇形ADC是一个圆锥的侧面展开图，则该圆锥的底面面积为

（结果保留π）；
④若E（7，0），试判断直线EC与⊙D的位置关系并说明你的理由．

（2012•峨边县模拟）如图在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．
（1）请完成如下操作：
①以点O为坐标原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系； ②根据图形提供的信息，标出该圆弧所在圆的圆心D，并连接AD、CD．
（2）请在（1）的基础上，完成下列填空：
①写出点的坐标：C

；
②⊙D的半径=

（结果保留根号）；
③若E（7，0），试判断直线EC与⊙D的位置关系，并说明你的理由．

（2013•江西）某学校活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：
●操作发现：
在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是

（填序号即可）
①AF=AG=

AB；②MD=ME；③整个图形是轴对称图形；④∠DAB=∠DMB．
●数学思考：
在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD和ME，则MD与ME具有怎样的数量和位置关系？请给出证明过程；
●类比探究：
在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD和ME，试判断△MED的形状．答：

等腰直角三角形

等腰直角三角形