题目内容
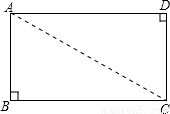
 如图,矩形纸片ABCD中,AB=8cm,AD=6cm,把矩形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,则AF的长度为________.
如图,矩形纸片ABCD中,AB=8cm,AD=6cm,把矩形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,则AF的长度为________.

分析:首先根据勾股定理计算出AC的长,再根据折叠的方法可得△ABC≌△AEC,△ADF≌△CEF,进而可得到可知AE=AB=8cm,CE=BC=AD=6cm,再设AF=x,则EF=DF=(8-x)cm,
在Rt△ADF中利用勾股定理可得62+(8-x)2=x2,再解方程即可.
解答:∵四边形ABCD是矩形,AD=6cm,
∴BC=AD=6cm,
∵AB=8cm,
∴AC=
 =10cm,
=10cm,矩形纸片沿直线AC折叠,则△ABC≌△AEC,△ADF≌△CEF,
可知AE=AB=8cm,CE=BC=AD=6cm,
设AF=x,则EF=DF=(8-x)cm,
在Rt△ADF中,
AD2+DF2=AF2,
即:62+(8-x)2=x2,
解得x=
 .
.故答案为:
 .
.点评:此题主要考查了矩形的性质、折叠的对称性、勾股定理及三角形的全等的性质,关键是掌握折叠以后有哪些线段是对应相等的.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
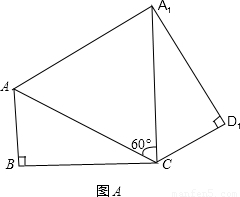
 如图,矩形纸片ABCD中,AB=4,BC=4
如图,矩形纸片ABCD中,AB=4,BC=4
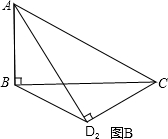

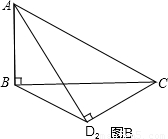
 把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E. ,将矩形沿对角线AC剪开,解答以下问题:
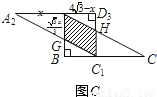
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



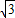 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: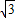 ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.