Question

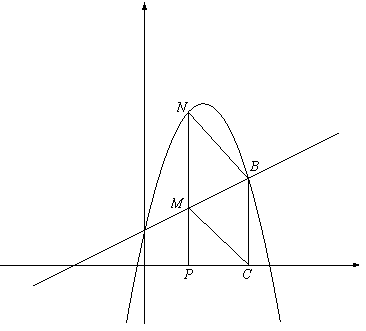
如图，抛物线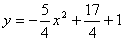与y轴交于A点，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C(3，0).

（1）求直线AB的函数关系式；

（2）动点P在线段OC上从原点出发以每秒一个单位的速度向C移动，过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N. 设点P移动的时间为t秒，MN的长度为s个单位，求s与t的函数关系式，并写出t的取值范围；

（3）设在（2）的条件下（不考虑点P与点O，点C重合的情况），连接CM，BN，当t为何值时，四边形BCMN为平行四边形？问对于所求的t值，平行四边形BCMN是否菱形？请说明理由.

 

Answer 1

略解：（1）易知A(0,1)，B(3,2.5)，可得直线AB的解析式为y=

（2）

（3）若四边形BCMN为平行四边形，则有MN=BC，此时，有

，解得，

 所以当t=1或2时，四边形BCMN为平行四边形.

①当t=1时，，，故,

又在Rt△MPC中，，故MN=MC，此时四边形BCMN为菱形

②当t=2时，，，故,

又在Rt△MPC中，，故MN≠MC，此时四边形BCMN不是菱形.