题目内容
 如图所示,在边长为2的菱形ABCD中,∠DAB=60°,点E为AB中点,点F是AC上一动点,则EF+BF的最小值为
如图所示,在边长为2的菱形ABCD中,∠DAB=60°,点E为AB中点,点F是AC上一动点,则EF+BF的最小值为分析:首先连接DB,DE,设DE交AC于M,连接MB,DF.证明只有点F运动到点M时,EF+BF取最小值,再根据菱形的性质、勾股定理求得最小值.
解答:解:连接DB,DE,设DE交AC于M,连接MB,DF,

∵四边形ABCD是菱形,
∴AC,BD互相垂直平分,
∴点B关于AC的对称点为D,
∴FD=FB,
∴FE+FB=FE+FD≥DE.
只有当点F运动到点M时,取等号(两点之间线段最短),
△ABD中,AD=AB,∠DAB=60°,
∴△ABD是等边三角形.
∵E为AB的中点,
∴DE⊥AB,
∴AE=
AD=1,DE=
=
=
,
∴EF+BF的最小值为
.

∵四边形ABCD是菱形,
∴AC,BD互相垂直平分,
∴点B关于AC的对称点为D,
∴FD=FB,
∴FE+FB=FE+FD≥DE.
只有当点F运动到点M时,取等号(两点之间线段最短),
△ABD中,AD=AB,∠DAB=60°,
∴△ABD是等边三角形.
∵E为AB的中点,
∴DE⊥AB,
∴AE=
| 1 |
| 2 |
| AD2-AE2 |
| 22-12 |
| 3 |
∴EF+BF的最小值为
| 3 |
点评:此题主要考查菱形是轴对称图形的性质,容易出现错误的地方是对点F的运动状态不清楚,无法判断什么时候会使EF+BF成为最小值.

练习册系列答案
相关题目
如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
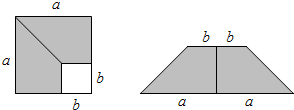

| A、(a-b)2=a2-2ab+b2 | B、(a+b)2=a2+2ab+b2 | C、a2-b2=(a+b)(a-b) | D、a2+ab=a(a+b) |

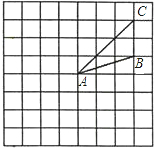 如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′,并计算对应点B和B′之间的距离.
如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′,并计算对应点B和B′之间的距离. 如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.
如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.