题目内容
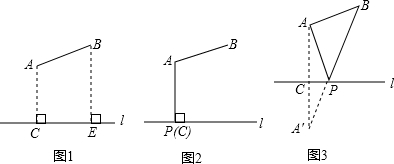
 如图,我们设计了一张帆布折椅,它的侧面如图所示,∠A=28°,∠ABC=64°,∠BCD=46°,∠D=12°,试求椅面AE和椅背DE的夹角∠AED的度数.
如图,我们设计了一张帆布折椅,它的侧面如图所示,∠A=28°,∠ABC=64°,∠BCD=46°,∠D=12°,试求椅面AE和椅背DE的夹角∠AED的度数.分析:延长DE交AB于F,利用三角形的内角和定理求出∠2,根据对顶角相等可得∠1=∠2,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答: 解:如图,延长DE交AB于F,
解:如图,延长DE交AB于F,
∵∠ABC=64°,∠BCD=46°,
∴∠2=180°-∠ABC-∠BCD=180°-64°-46°=70°,
∴∠1=∠2=70°,
∴∠3=∠D+∠1=12°+70°=82°,
∠AED=∠A+∠3=28°+82°=110°.
 解:如图,延长DE交AB于F,
解:如图,延长DE交AB于F,∵∠ABC=64°,∠BCD=46°,
∴∠2=180°-∠ABC-∠BCD=180°-64°-46°=70°,
∴∠1=∠2=70°,
∴∠3=∠D+∠1=12°+70°=82°,
∠AED=∠A+∠3=28°+82°=110°.
点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,熟记性质并作辅助线构造出三角形是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 的大小比较,有下面的方法:
的大小比较,有下面的方法: 时,一定有
时,一定有 ;
; 时,一定有
时,一定有 ;
; 时,一定有
时,一定有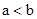 .
.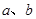 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较: ,
,
 )与(
)与( )的符号相同
)的符号相同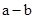 >0,得
>0,得
 的大小比较,有下面的方法:
的大小比较,有下面的方法: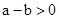 时,一定有
时,一定有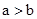 ;
; 时,一定有
时,一定有 ;
;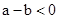 时,一定有
时,一定有 .
. 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较: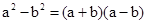 ,
,
 )与(
)与( )的符号相同
)的符号相同 >0,得
>0,得