Question

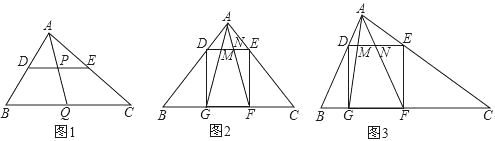
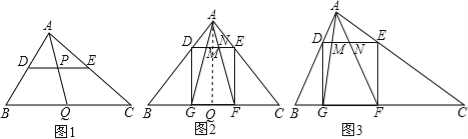
【题目】（1）如图1，在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE∥BC，AQ交DE于点P，求证： ；

（2）如图，△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG，AF分别交DE于M，N两点．

①如图2，若AB=AC=1，直接写出MN的长；

②如图3，求证：MN2=DM·EN．

Answer 1

【答案】（1）证明见解析；（2）MN=．证明见解析．

【解析】试题分析：（1）可证明△ADP∽△ABQ，△ACQ∽△ADP，从而得出=；

（2）①根据三角形的面积公式求出BC边上的高，根据△ADE∽△ABC，求出正方形DEFG的边长，根据等于高之比即可求出MN；

②可得出△BGD∽△EFC，则DGEF=CFBG；又由DG=GF=EF，得GF2=CFBG，再根据（1）==，从而得出答案．

（1）证明：在△ABQ和△ADP中，

∵DP∥BQ，

∴△ADP∽△ABQ，

∴=，

同理在△ACQ和△APE中，

=，

∴=．

（2）①作AQ⊥BC于点Q．

∵BC边上的高AQ=，

∵DE=DG=GF=EF=BG=CF

∴DE：BC=1：3

又∵DE∥BC，

∴AD：AB=1：3，

∴AD=，DE=，

∵DE边上的高为，MN：GF=：，

∴MN：=：，

∴MN=．

故答案为：．

②证明：∵∠B+∠C=90°∠CEF+∠C=90°，

∴∠B=∠CEF，

又∵∠BGD=∠EFC，

∴△BGD∽△EFC，

∴=，

∴DGEF=CFBG，

又∵DG=GF=EF，

∴GF2=CFBG，

由（1）得==，

∴×=，

∴（）2=，

∵GF2=CFBG，

∴MN2=DMEN．