题目内容
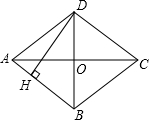 如图,菱形 ABCD对角线AC=6cm,BD=8cm,则菱形高DH长为( )
如图,菱形 ABCD对角线AC=6cm,BD=8cm,则菱形高DH长为( )| A、5cm | B、4.8cm | C、10cm | D、9.6cm |
分析:根据菱形面积=
AC•BD=AB•DH,继而将问题转化为求菱形的边长,在Rt△AOD中,利用勾股定理即可求出.
| 1 |
| 2 |
解答:解:∵AC=6cm,BD=8cm,
∴AO=3cm,DO=4cm,
在Rt△AOD中,根据勾股定理得:AD2=AO2+DO2,
即AD2=32+42,解得:AD=5cm,
∴AB=AD=5cm,
又菱形面积=
AC•BD=AB•DH,
代入各线段的长得:
×6×8=5×DH,
解得:DH=4.8cm.
故选B.
∴AO=3cm,DO=4cm,
在Rt△AOD中,根据勾股定理得:AD2=AO2+DO2,
即AD2=32+42,解得:AD=5cm,
∴AB=AD=5cm,
又菱形面积=
| 1 |
| 2 |
代入各线段的长得:
| 1 |
| 2 |
解得:DH=4.8cm.
故选B.
点评:本题考查菱形的性质,难度适中,解题关键是掌握菱形面积的计算公式.

练习册系列答案
相关题目


 (2012•丰台区二模)已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是2,求菱形ABCD的周长.
(2012•丰台区二模)已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是2,求菱形ABCD的周长. 如图,菱形ABCD中,点O是对角线AC上一点,OA=AD,且OB=OC=OD=1,则该菱形的边长为( )
如图,菱形ABCD中,点O是对角线AC上一点,OA=AD,且OB=OC=OD=1,则该菱形的边长为( ) 如图,菱形ABCD中,对角线AC,BD相交于O点,OE⊥AB,垂足为E,以O为圆心,OE为半径作⊙O.试说明⊙O与CD相切.
如图,菱形ABCD中,对角线AC,BD相交于O点,OE⊥AB,垂足为E,以O为圆心,OE为半径作⊙O.试说明⊙O与CD相切.