Question

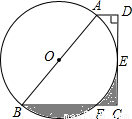
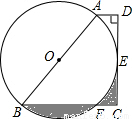
（2004•武汉）如图，梯形ABCD中，AD∥BC，∠D=90°，以AB为直径的⊙O与CD相切于E，与BC相交于F，若AB=4，AD=1，则图中两阴影部分面积之和为    ．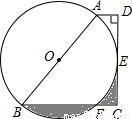

Answer 1

【答案】分析：梯形DAOE的面积-扇形AOE的面积=梯形中的阴影面积；小弓形的面积=扇形OBF的面积-△OBF的面积，让两个阴影相加即可．
解答：解：连接OE，作AG⊥OE于点G．
由已知可知，OA=2，AD=1，OE=2，
∴OG=1，
∴AG=，∠AOE=60°，
∵梯形中阴影面积=（2+1）×÷2-=-；
小弓形阴影面积=-2×÷2=-，
∴两阴影部分相加=．
点评：本题的难点是根据所给的已知条件求出梯形的下底，直角腰的长，及扇形的圆心角的度数；关键是得到阴影的组成．