Question

a、b都是有理数，现有4个判断：①如果a+b＜a，则b＜0；②如果ab＜a，则b＜0；③如果a-b＜a，则b＞0；④如果a＞b，则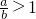，其中正确的判断是

1. A.
   ①②
2. B.
   ②③
3. C.
   ①④
4. D.
   ①③

Answer 1

D
分析：①利用不等式性质1，同减去a，不等号不变，故正确；②若a＜0，利用不等式性质3，同除以a，不等号改变，故错误；③先利用不等式性质1，同减去a，方向不变，再利用不等式性质3，同乘以-1，方向改变，故正确；④若b＜0，利用不等式性质3，同除以b，不等号方向改变，故错误．
解答：①∵a+b＜a，
∴b＜0（不等式性质1），
故此选项正确；
②∵ab＜a，
若a＜0，
∴b＞0（不等式性质3），
故此选项错误；
③∵a-b＜a，
∴-b＜0（不等式性质1），
∴b＞0（不等式性质3），
故此选项正确；
④∵a＞b，
若b＜0，
∴＜1（不等式性质3），
故此选项错误．
故正确的是①③．
故选D．
点评：不等式的性质：
（1）不等式两边加（或减）同一个数（或式子），不等号的方向不变．
（2）不等式两边乘（或除以）同一个正数，不等号的方向不变．
（3）不等式两边乘（或除以）同一个负数，不等号的方向改变．