题目内容
解不等式组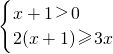 ,判断x=
,判断x= 是否满足该不等式组,并说明理由.
是否满足该不等式组,并说明理由.
解: ,
,
由①得,x>-1,
由②得,x≤2,
则不等式组的解集为-1<x≤2.
∵ >0,
>0,
( )2=
)2= <2,
<2,
∴-1< ≤2.
≤2.
∴x= 满足该不等式组.
满足该不等式组.
分析:根据不等式的性质,分别求出两个不等式的解集,再求其公共部分,然后验证x= 是否满足该不等式组.
是否满足该不等式组.
点评:此题主要考查了此题考查了不等式组的解集,求不等式的公共解,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.
 ,
,由①得,x>-1,
由②得,x≤2,
则不等式组的解集为-1<x≤2.
∵
 >0,
>0,(
 )2=
)2= <2,
<2,∴-1<
 ≤2.
≤2.∴x=
 满足该不等式组.
满足该不等式组.分析:根据不等式的性质,分别求出两个不等式的解集,再求其公共部分,然后验证x=
 是否满足该不等式组.
是否满足该不等式组.点评:此题主要考查了此题考查了不等式组的解集,求不等式的公共解,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
 并判断
并判断 是否为该不等式组的解.
是否为该不等式组的解. 并判断
并判断 是否为该不等式组的解.
是否为该不等式组的解.  并判断
并判断 是否为该不等式组的解.
是否为该不等式组的解.