Question

【题目】如图，B、D、E、F是直线 l上四点，在直线 l的同侧作△ABE和△CDF，且 AB∥CD，∠A=40°．作BG⊥AE于 G，FH⊥CD于 H，BG与 FH交于 P点．

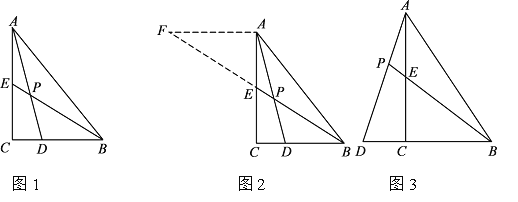
（1）如图 1，B、E、D、F从左至右顺次排列，∠ABD=90°，求∠GPH；

（2）如图 2，B、E、D、F从左至右顺次排列，△ABE与△CDF均为锐角三角形，求∠GPH；

（3）如图 3，F、B、E、D从左至右顺次排列，△ABE为锐角三角形，△CDF为钝角三角形，则∠GPH的度 数为多少？请画出图形并直接写出结果，不需证明．

Answer 1

【答案】（1）40°；（2）140°；（3）40°.

【解析】

（1）由题意可根据直角三角形两锐角互余求出∠GPH=∠A=40°；

（2）延长CD与AE相交于点M，则PGMH为四边形，因为BG⊥AE于G，FH⊥CD于H，则∠PGE=∠PHD=90°，则∠P=360°-∠PGE°-∠PHD-∠M=360°-180°-∠M，又知AB∥CD，所以∠M=∠A=40°，则可以求得∠P的度数；

（3）根据题意可以作图，延长AB与FH相交于点M，因为AB∥CD，所以∠CHF=∠BMP=90°，则根据三角形内角和定理可得∠GPH=∠A=40°．

（1）∵BG⊥AE，

∴∠BGE=90°

∴∠GBE+∠GEB=90°

∵FH⊥CD, AB∥CD，

∴AB⊥BE,

∴∠ABE=90°

∴∠A+∠AEB=90°，

∴∠GPH=∠GBE=∠A=40°；

（2）如图所示：

∵AB∥CD，

∴∠M=∠A=40°．

延长CD与AE相交于点M．

则在四边形PGMH中∠P=360°-180°-∠M=360°-∠A-180°=140°；

（3）∠GPH=40°，图如下边所示：

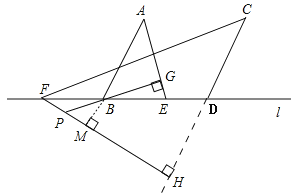
延长AB与FH相交于点M，

因为AB∥CD，

所以∠CHF=∠BMP=90°，

∵PG⊥AE，

∴∠BAG+∠ABG=90°，∠PBM+∠BPM=90°，

∵∠ABG=∠PBM，

∴∠BPM=∠A，

即∠GPH=∠A=40°．