题目内容
6.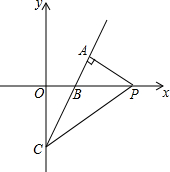 如图,在平面直角坐标系中,直线y=2x+b经过点A(2,1),分别交x轴、y轴于点B,C
如图,在平面直角坐标系中,直线y=2x+b经过点A(2,1),分别交x轴、y轴于点B,C(1)求点B与点C的坐标;
(2)若点P是x轴上一点,且满足△PAC的面积是4,求点P的坐标.
分析 (1)把点A的坐标代入函数解析式,利用待定系数法求得b的值;然后结合函数解析式来求电费B、C的坐标即可;
(2)由三角形的面积公式来求点P的坐标.
解答  解:(1)把点A(2,1)代入y=2x+b,得
解:(1)把点A(2,1)代入y=2x+b,得
1=2×2+b,
解得b=-3,
则该直线方程为:y=2x-3.
当x=0时,y=-3,即C(0,-3).
当y=0时,x=$\frac{3}{2}$,即B($\frac{3}{2}$,0);
(2)设P(a,0),则PB=(|a-$\frac{3}{2}$|,0),
故S△PAC=$\frac{1}{2}$×|a-$\frac{3}{2}$|×4=4,
解得a=$\frac{7}{2}$或a=-$\frac{1}{2}$
故点P的坐标是($\frac{7}{2}$,0)或(-$\frac{1}{2}$,0).
点评 本题考查了一次函数图象上点的坐标特征.一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11.一个鸡蛋的质量约( )
| A. | 20g | B. | 60g | C. | 200g | D. | 1kg |
 一水库大坝的横断面为梯形ABCD,坝顶宽6.2米,坝高23.5米,斜坡AB的坡度iAB=1:3,斜坡CD的坡角是21°,求:
一水库大坝的横断面为梯形ABCD,坝顶宽6.2米,坝高23.5米,斜坡AB的坡度iAB=1:3,斜坡CD的坡角是21°,求: 如图,已知∠AOB为锐角,∠AOD=∠BOC=90°,OM,ON分别是∠AOB和∠COD的平分线.
如图,已知∠AOB为锐角,∠AOD=∠BOC=90°,OM,ON分别是∠AOB和∠COD的平分线.