题目内容
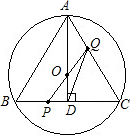
 如图,从等边三角形内一点向三边作垂线,已知这三条垂线段的长分别为1、3、5,则这个等边三角形的边长为
如图,从等边三角形内一点向三边作垂线,已知这三条垂线段的长分别为1、3、5,则这个等边三角形的边长为分析:作AM⊥BC,根据等边三角形的面积计算可以求得AM=PE+PD+PF,再根据等边三角形的高线长可以计算等边三角形的边长,即可解题.
解答: 解:过A作AM⊥BC,则AM为BC边上的高,
解:过A作AM⊥BC,则AM为BC边上的高,
连接PA、PB、PC,
则△ABC的面积S=
BC•AM=
(BC•PD+AB•PF+AC•PE),
∴BC•AM=BC•PD+AB•PF+AC•PE,
∵△ABC是等边三角形,
∴AB=BC=AC,
∴BC•AM=BC•PD+BC•PF+BC•PE=BC•(PD+PF+PE),
∴PD+PE+PF=AM,
∴△ABC的高为:1+3+5=9,
∴△ABC的边长为:AB=
=
=9×
=6
,
故答案为6
.
 解:过A作AM⊥BC,则AM为BC边上的高,
解:过A作AM⊥BC,则AM为BC边上的高,连接PA、PB、PC,
则△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
∴BC•AM=BC•PD+AB•PF+AC•PE,
∵△ABC是等边三角形,
∴AB=BC=AC,
∴BC•AM=BC•PD+BC•PF+BC•PE=BC•(PD+PF+PE),
∴PD+PE+PF=AM,
∴△ABC的高为:1+3+5=9,
∴△ABC的边长为:AB=
| AM |
| sin∠ABC |
| 9 | ||||
|
| 2 | ||
|
| 3 |
故答案为6
| 3 |
点评:本题考查了三角形面积的计算,考查了等边三角形边长和高线长的关系,本题中求AM=PD+PE+PF是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目

 终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,设它们运动的时间为x(s).
终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,设它们运动的时间为x(s).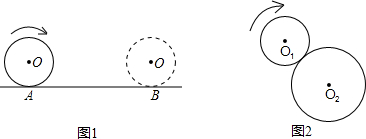
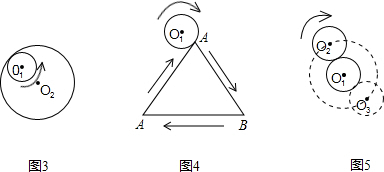
 如图,等边三角形和正方形的边长都是a,在图形所在的平面内,将△PAD以点A为中心沿逆时针方向旋转,使AP与AB重合,如此继续分别以点B、C、D 为中心将三角形进行旋转,使点P回到原来位置为止,则点P从开始到结束所经过路径的长为( )
如图,等边三角形和正方形的边长都是a,在图形所在的平面内,将△PAD以点A为中心沿逆时针方向旋转,使AP与AB重合,如此继续分别以点B、C、D 为中心将三角形进行旋转,使点P回到原来位置为止,则点P从开始到结束所经过路径的长为( )